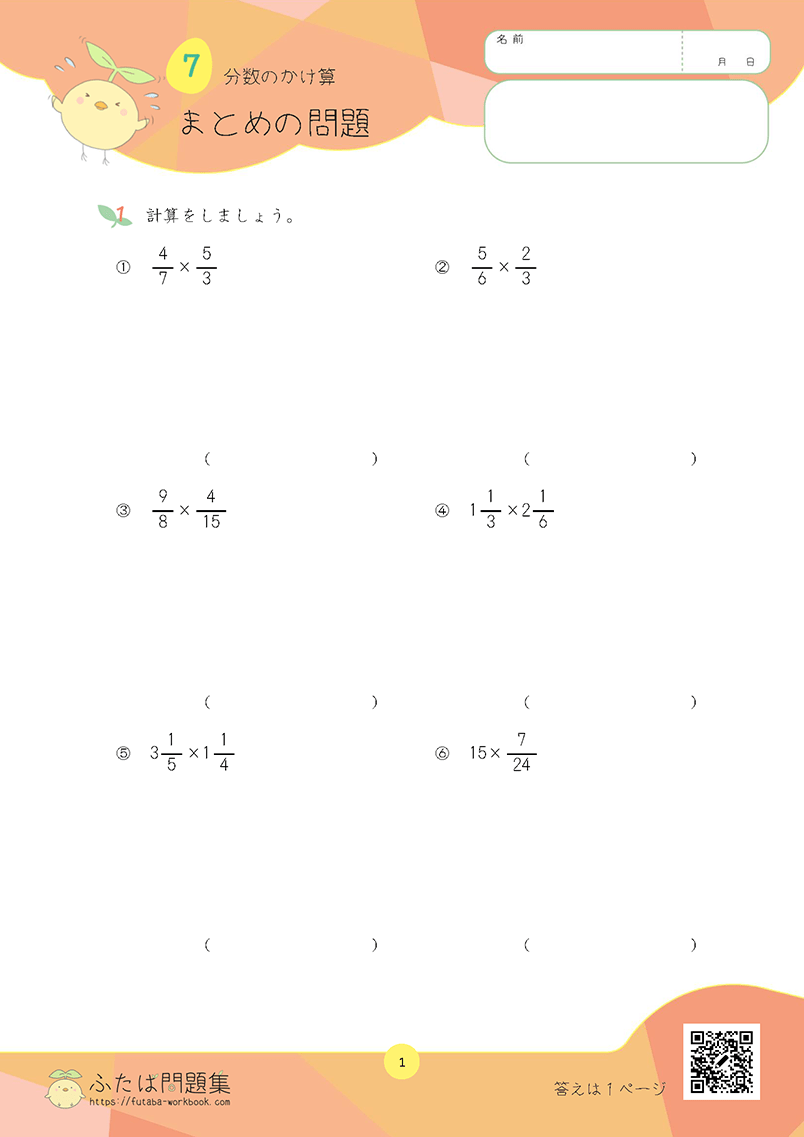正多角形を正しく理解しましょう
小学5年生の第17章「正多角形と円周の長さ」です。
この章は、正多角形を円の性質と関連づけて考える学習です。
さらに、円周率を活用して、円周の長さも求めます。
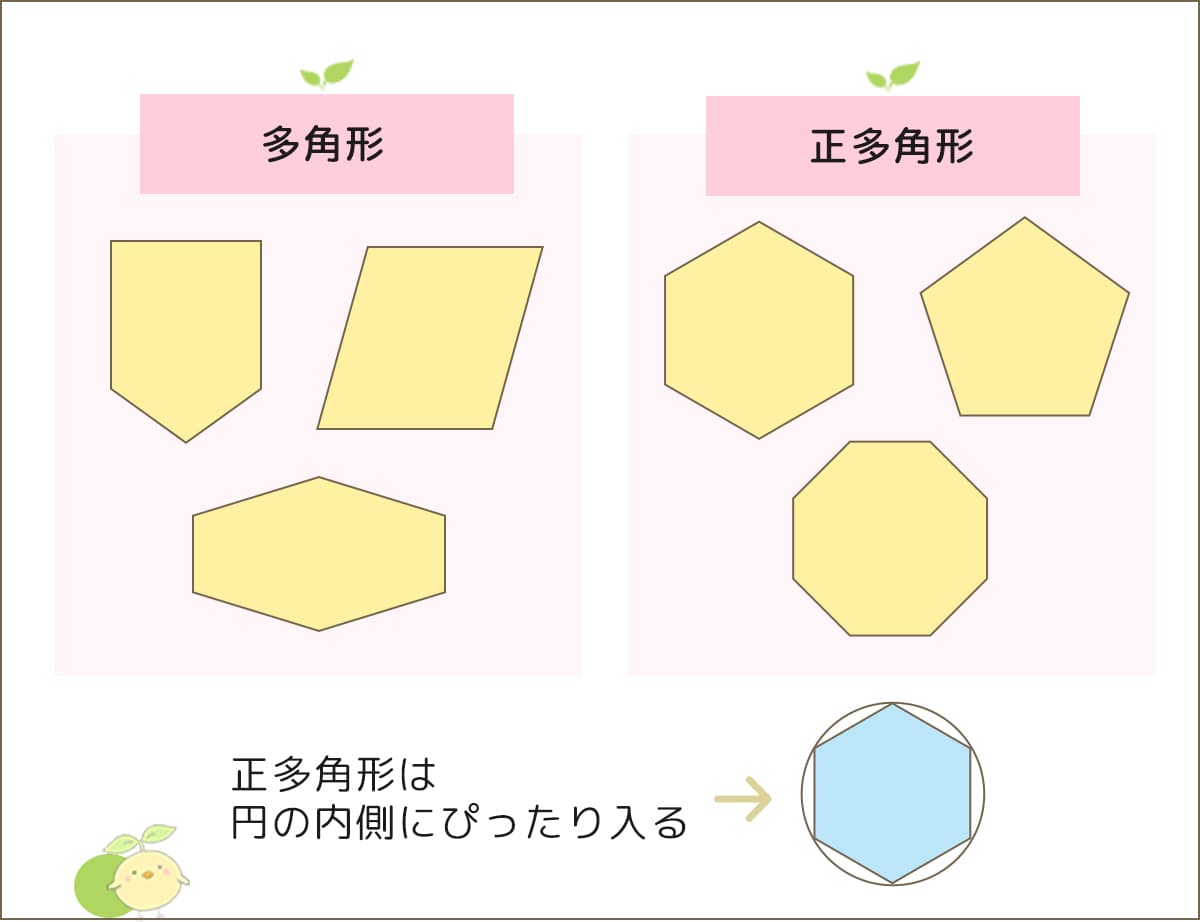
まずは、多角形と正多角形のちがいをおぼえましょう。
- 多角形:三つ以上の直線で囲まれた図形である
- 正多角形:辺の長さがすべて等しく,角の大きさがすべて等しい多角形
さらに、正多角形を理解するために、円の性質と関連づけて考えましょう。
- 正多角形は、円の内側にぴったり入る(円に内接する)
- 正多角形は、円の外側にぴったり接する(円に外接する)
これらの性質があるため、以下のことがいえます。
- 円に内接する正八角形の頂点と円の中心とを結ぶと、8つの二等辺三角形ができる
- 6つの合同な正三角形を一つの頂点が共通になるように並べると正六角形ができる
円の性質と関連づけながら、正多角形を正しく理解しましょう。
それぞれの角度を求められるようにしましょう
正多角形の学習では、分度器を使わずに角度を求める問題が出題されます。
このときは、円や三角形の性質を活用することがポイントです。
とくに「三角形の3つの角の大きさの和が 180 度である」ことはおぼえておきましょう。
例えば、四角形の角の大きさの和を求められます。
- 四角形は、2つの三角形からできている
- つまり、四角形の角の大きさの和は、180度の2倍
- だから、四角形の角の大きさの和は360度
このように、「三角形の3つの角の大きさの和が 180 度」を活用すれば、ほかの多角形の角度を求められるのです。
プラスで正三角形や二等辺三角形の角の性質も思い出しながら、問題にチャレンジしてみましょう。
円周の長さを求められるようにしましょう
円周の長さを求めるためには、「円周率(3.14)」を使います。
まずは、公式をおぼえましょう。
「円周」=「直径」×「円周率(3.14)」
つまり、直径が2倍・3倍になると、円周も2倍・3倍になるといえます。
公式をおぼえれば、式を立てることはむずかしくありません。
くれぐれも計算ミスをしないように気をつけましょう。
多角形の角についての性質は、中学2年生でさらに学習を深めていきます。
多くの問題を解いて、正多角形や円の性質をしっかり理解しましょう。
![]() 無料算数学習プリント
無料算数学習プリント
ふたば問題集
小学5年生 第17章「正多角形と円周の長さ」