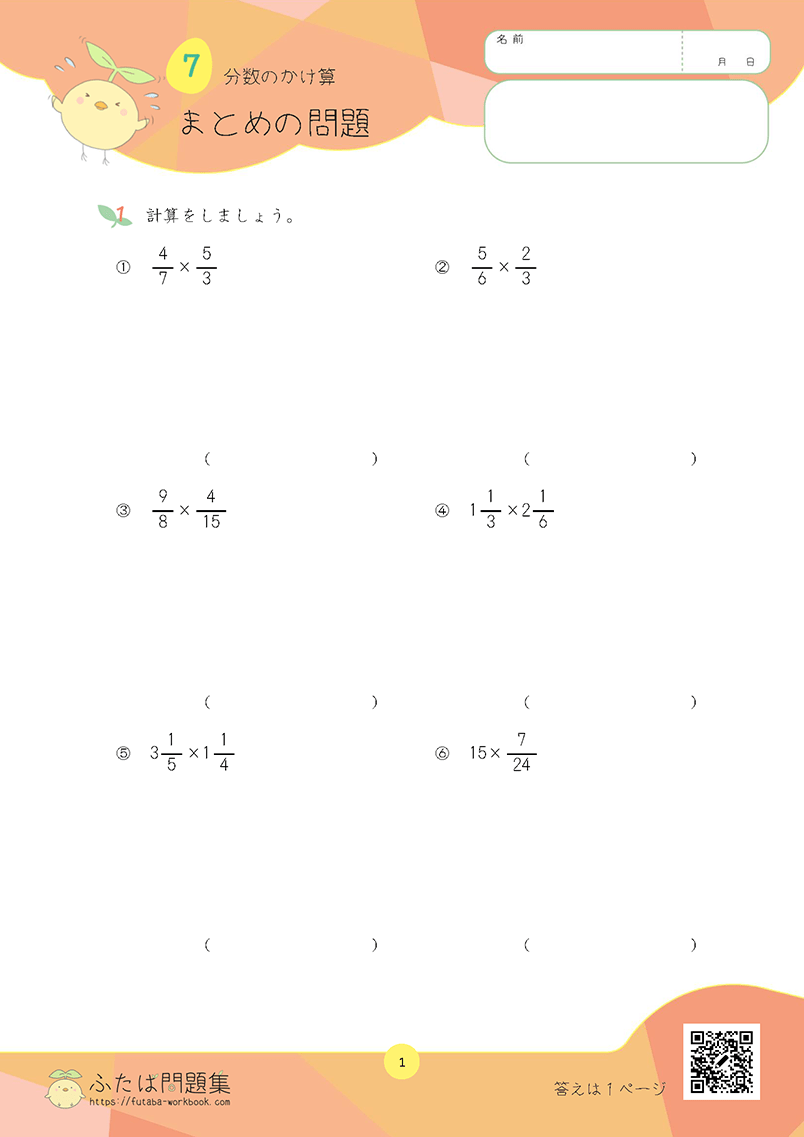割合を理解しましょう
第14章「割合」では、割合を使って二つのものを比べることや、百分率を用いた表し方について学習します。
- 割合とは、もとにする量を1としたときに、比べる量がどれくらいかを表すもの
- 割合＝比べる量÷もとにする量
この2点は、かならず覚えておきましょう。
例えば「シュートのうまさ」を比べるときも、割合が便利です。
- 10回シュートをうって、6本シュートが入った人
- 20回シュートをうって、10本シュートが入った人
この場合「シュートが入った数の差」では比べられないですよね。
しかし「全シュート数（もとにする量）」と「入ったシュート数（比べる量）」の二つの数量関係を表した割合を使えば、シュートのうまさを比べられます。
- 10 回中6回入った人の割合：6÷10＝0.6
- 20回中10回入った人の割合：10÷20＝ 0.5
- 「10 回中6回入った人」のほうがシュートがうまい
まずは問題を解きながら、割合の便利さやおもしろさを実感しましょう。
式をたてるのがむずかしい場合は、線分図をかいて整理するのがおすすめです。
百分率を求められるようにしましょう
百分率とは、50％や90％など、100をもとにしてあらわしたものです。
小数や整数で表した割合に、100をかけて求めます。
例えば、先ほどのシュートの割合「0.6」の場合で考えてみましょう。
- 0.6×100＝60
- シュートの成功確率は60％
クイズの正答率や天気予報の降水確率、打率やシュート率など、身近にある百分率をさがして理解を深めましょう。
割合の学びは、6年生の比、中学校における「数と式」や「関数」、中学校の理科における考察につながります。
多くの問題を解いて、割合をマスターしましょう。
