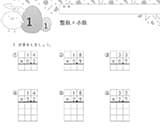
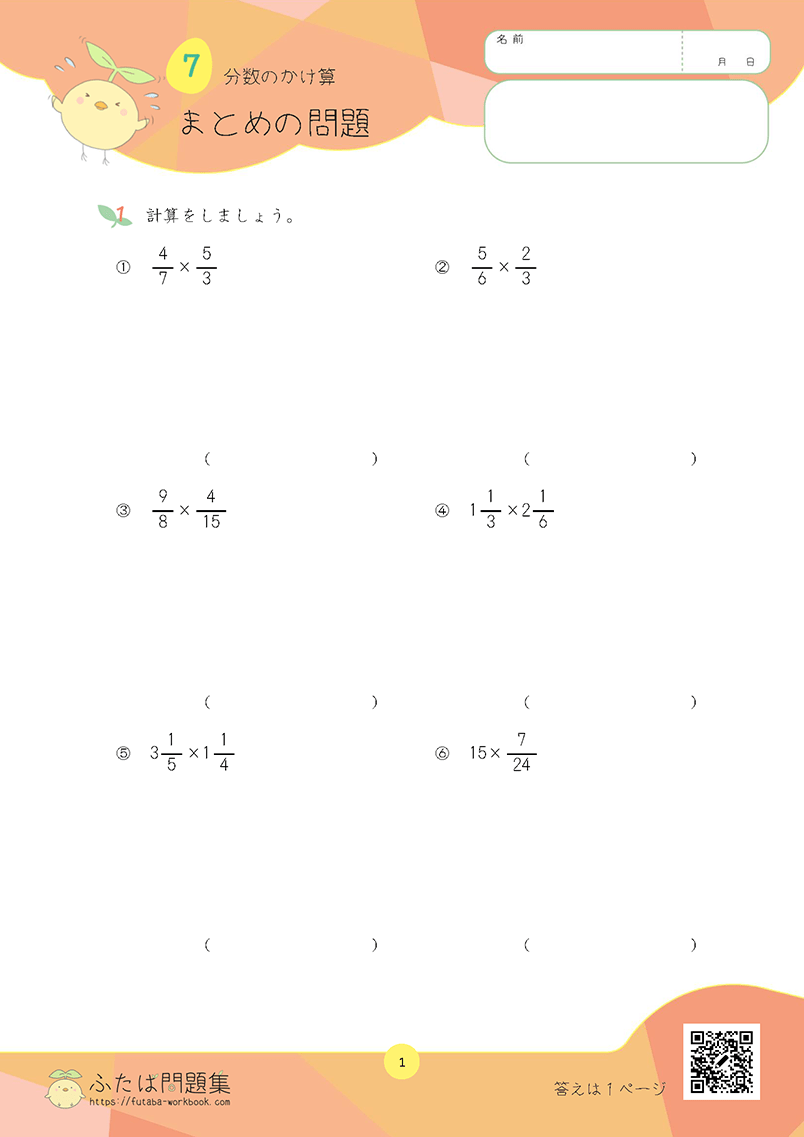約分をできるようにしましょう
第10章「分数のたし算とひき算」です。
この章は分数のたし算やひき算を計算できるようになる学習となります。
まずは、約分について理解しましょう。
約分とは、分子と分母それぞれを同じ数でわることです。
公約数や最大公約数を活用するのがポイントになります。
例えば、$\frac{4}{10}$ の場合で考えてみましょう。
- 4と10の公約数は2
- 分子を2でわる：4÷2=2
- 分母を2でわる：10÷2=5
- 約分すると、$\frac{2}{5}$
やり方を覚えて、練習しましょう。
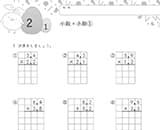
通分をできるようにしましょう
次は、通分について確認します。
通分とは、2つ以上の分数の分母をそろえることを意味します。
公倍数や最小公倍数を活用するのがポイントです。
例えば、$\frac{2}{3}$と$\frac{4}{5}$で考えてみましょう。
- 分母の3と5の最小公倍数は「15」
- 分母を「15」にそろえる
- $\frac{2}{3}$の場合：分母は3×5＝15だから、分子が2×5＝10
- $\frac{4}{5}$の場合：分母は5×3＝15だから、分子が4×3＝12
- $\frac{2}{3}$と$\frac{4}{5}$を通分すると、$\frac{10}{15}$と$\frac{12}{15}$になる
分子と分母にそれぞれ同じ数をかけても、分数の大きさはかわりません。
この特徴が通分にも生かされていますね。
通分は分数のたし算やひき算で必要なスキルなので、何度も練習しましょう。
分数のたし算とひき算を求められるようにしましょう
分数のたし算とひき算で大切なのは、「必ず同じ分母どうしで計算すること」です。
$\frac{2}{3}$と$\frac{4}{5}$の場合でみていきましょう。
よくあるまちがいは、分子は「2＋4」、分母は「3＋5」と計算してしまうことです。
分数のかけ算とは、別物であることを理解することが大切です。
- まず、通分する
- $\frac{2}{3}$と$\frac{4}{5}$を通分すると、$\frac{10}{15}$と$\frac{12}{15}$になる
- $\frac{10}{15}$は$\frac{1}{15}$が10こ分、$\frac{12}{15}$は$\frac{1}{15}$が15こ分
- $\frac{10}{15}$＋$\frac{12}{15}$は、10＋15＝25だから$\frac{1}{15}$が25こ分
- 答えは、$\frac{25}{15}$
- 5で約分すると、$\frac{5}{3}$
このように、通分や約分を活用して、解いていきましょう。
分数のたし算やひき算は、これからさまざま学習で必要とされる計算スキルです。
多くの問題を解いて、計算力をつけましょう。
無料学習プリント ふたば問題集
>第10章「分数のたし算とひき算」
