円の面積を正しく求められるようにしましょう
第8章「円の面積」です。
この章は、円周率を使って円の面積を求める学習となります。
5年生では円周の長さを求める問題を学習しました。
では、それぞれの公式をもう一度みておきましょう。
- 「円周」＝「直径」×「円周率（3.14）」
- 「円の面積」＝「半径」×「半径」×「円周率（3.14）」
よくあるまちがいが、「円の面積」＝「直径」×「直径」×「円周率（3.14）」と計算してしまうことです。
正しく求められるように、それぞれの公式をしっかりおぼえておきましょう。
さらに、ここで注意しておくべきことがあります。
それは円の面積は、半径の長さが2倍・3倍になっても、同じように2倍・3倍にはならないことです。
例えば、半径10cmを10倍にすると、円の面積はいくらになるでしょうか。
- 「10cm」×「10cm」×「円周率（3.14）」＝314
- 「100cm」×「100cm」×「円周率（3.14）」＝31400
- つまり、10×10＝100倍になります。
これが、円周の長さの公式と円の面積の公式と大きくちがう点です。
問題を解くときは、注意しましょう。
複雑な図形の面積求められるようにしましょう
複雑な図形の面積を求めるときは、計算しやすいように図解を分解しましょう。
例えば、一見むずかしいと感じる図形も分解してみると、正方形と半円2つ（円1つ）で構成されていると気づくことがあります。
まずは、円や半円、三角形や四角形がかくれていないかをよく観察しましょう。
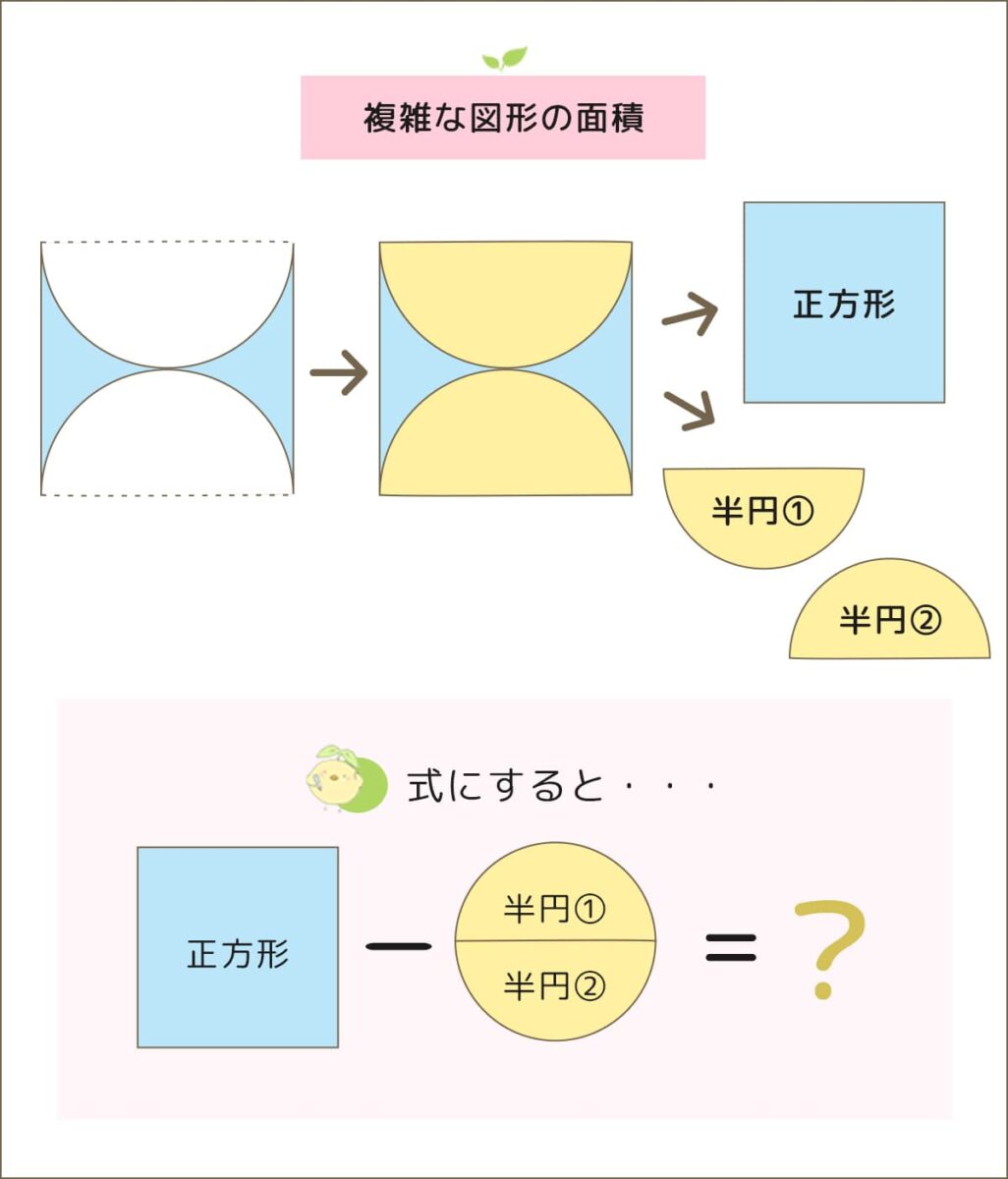
慣れるまでは、「□ー○」のように図形で式を書いて、解き方を整理することがおすすめです。
円の面積で身につけたスキルは、6年生の円柱の学習につながります。
多くの問題を解いて、円の面積をマスターしましょう。
無料学習プリント ふたば問題集
>第8章「円の面積」
