計算のきまりを理解しよう
小学2年生の第8章「計算のくふう」では、たし算の結合法則や交換法則といった計算のきまりを活用して、計算をくふうできるようにするのが目標です。
結合法則
- 3つの数のたし算では計算の順番を変えても答えは変わらない
- (a +b)+c = a +(b +c)
交換法則
- 「たされる数」と「たす数」を入れ替えて計算しても答えは変わらない
- a+b=b+a
2年生では、法則の名前を覚える必要はありませんが、計算のきまりがあることを理解しておきましょう。
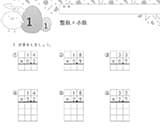
「10 のまとまり」に着目しよう
2年生の「計算のくふう」で大切なのは「10のまとまりになる数の組み合わせ」を見つけることです。
例えば「25+19+1」で考えてみましょう。
- 「25 +19+1」で「一の位を足して10になる数の組み合わせ」を考える
- 「 25 +(19 +1)」と計算を工夫する
- 「 25 +(19 +1)= 25 + 20 」
- 「 25 +(19 +1)= 45」
このように「10のまとまり」に着目し、()を使って計算の順番を変えれば、2年生でも計算のくふうができます。
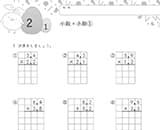
では、「65-6」の場合はどうでしょうか。
この場合も「10のまとまりになる数の組み合わせ」を見つけられるかどうかがポイントです。
- ひかれる数「65」から「5」をひけば「60」になる
- ひく数「6」を「5」と「1」にわけて計算する
- 「(65-5)-1」と計算をくふうする
- 「60-1=59」
たし算でもひき算でも「10のまとまり」に着目しましょう。
計算をくふうすることは2年生にとってはじめてであるため、むずかしいと感じることもあるかもしれません。
たくさん失敗してもいいので、計算のきまりを活用して計算する経験をできるだけ多く積み重ねることが大切です。
もし正解できなくても
- 「()を使おうとしたんだね」
- 「計算の順番を変えるのはいい考えだね」
- 「10のまとまり」を探そうとしているのがさすがだね
など、計算をくふうしようとする態度をたくさんほめてあげましょう。
![]() 無料算数学習プリント
無料算数学習プリント
ふたば問題集
小学2年生 第8章「計算のくふう」