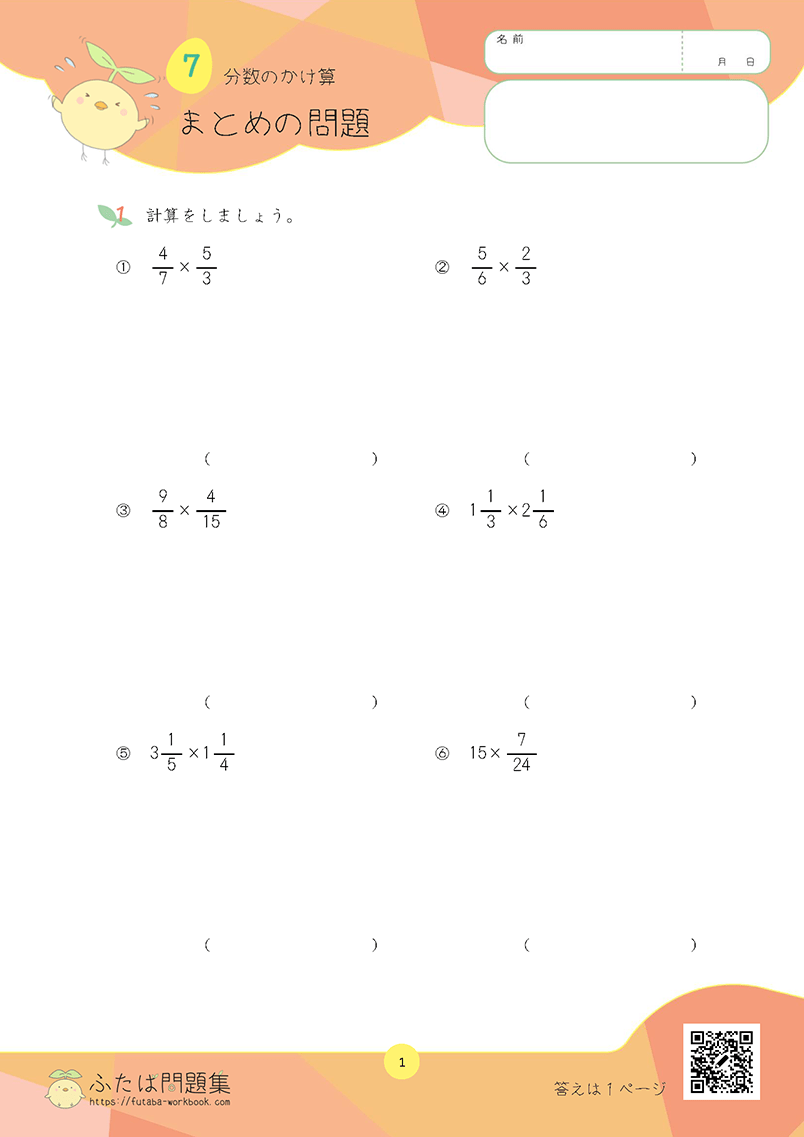「分母」と「分子」の違いを身に付けましょう
3年生の分数は子どもにとって難しい章の一つです。
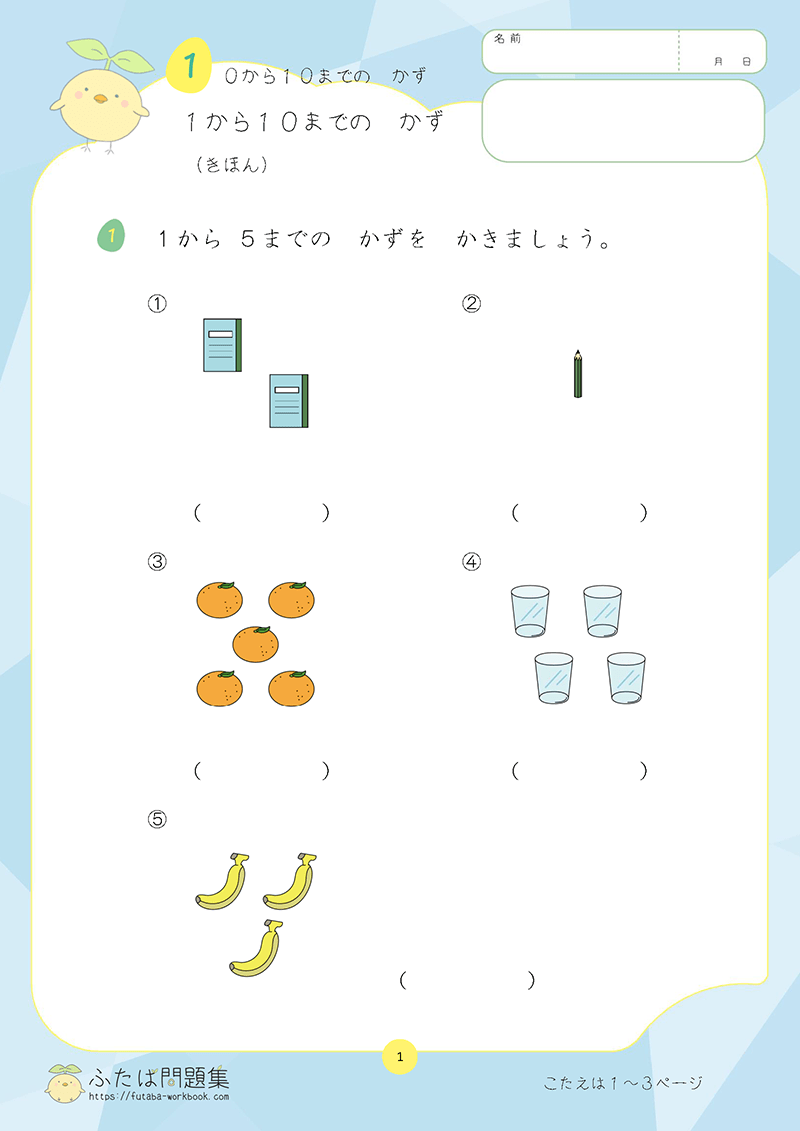
小学3年生の15章「分数」では、一つ一つ分数の意味やコツを確認しながら学んでいきましょう。
まず、分数を読むときは「2分の1」と分母から読みますね。
分数を書く時も、上に書く分子より下に書く分母の数字を先に書く習慣をつけると良いでしょう。
細かなコツですが、お子さんにとって分数の意味やその後の計算が分かりやすくなります。
「何を等分したのか」を確認しましょう
「等分する」というのは「同じ大きさに分ける」ということですが、大切なのは「何を等分したか」です。
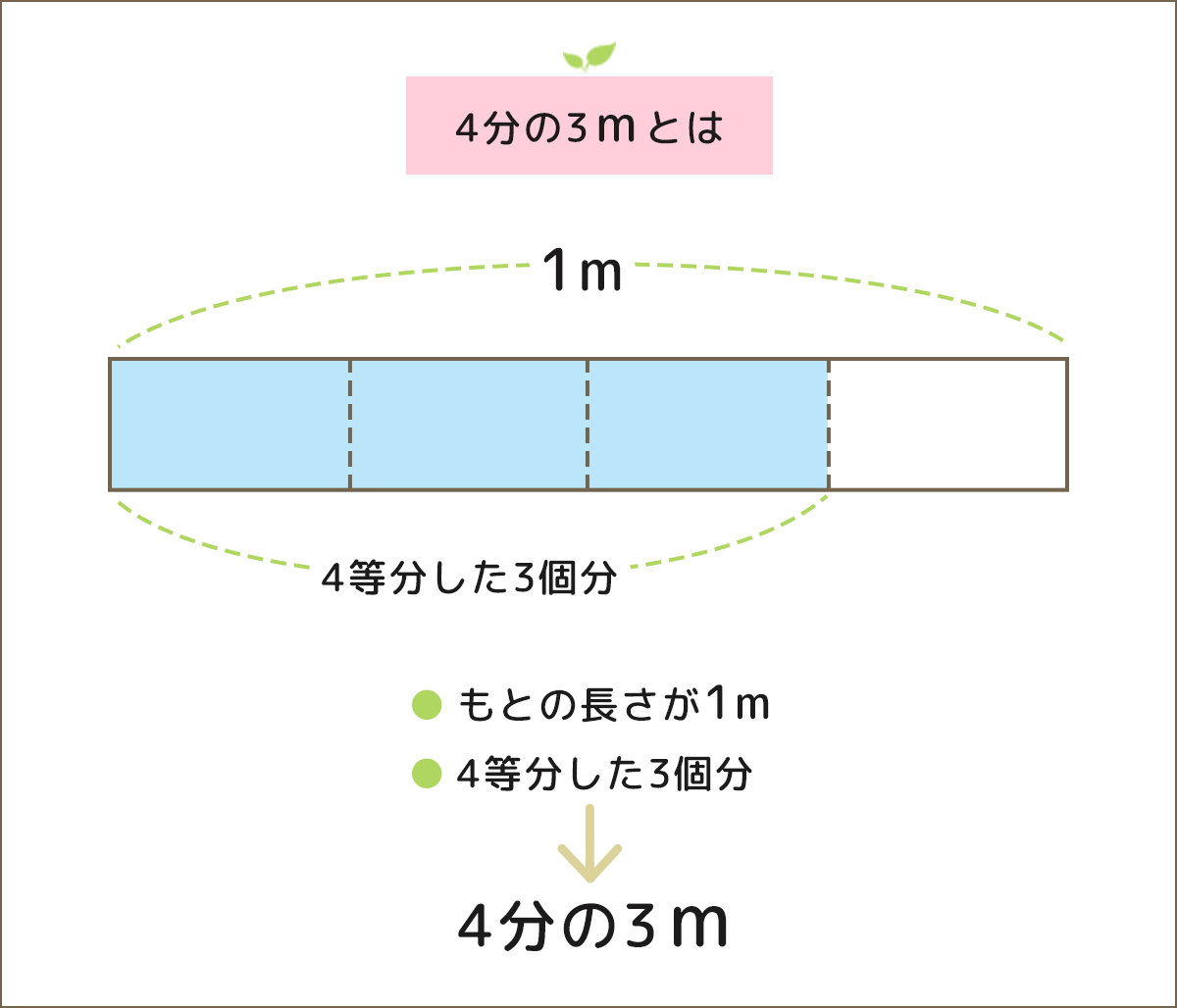
「2分の1ⅿ」は、もとの長さが1ⅿで、1ⅿを2等分した長さです。
テープ絵やテープ図の1ⅿを4等分した3個分は「4分の3m」ですが、その答えだけ考えるのではなく「もとの長さが1ⅿで・・」と意識して「もとの数」をお子さんに確認させてあげてください。
分数の基礎である「◯分の1」の考え方をもう一度復習したい場合は、2年生の分数にトライしてみましょう。
→小学2年生の「分数の基礎」
1をもとに分数を理解しましょう
数直線の問題がよく出てきます。
但しこの数直線の最後の目盛りは、1で終わっているわけではありません。
例えば、「5分の4」の目盛りは、「1をもとにして、1を5等分した4個分」となります。
その「1をもとに」という「1」を数直線上で確認することで、「5分の5」は「1を5等分した5個分」だから1と同じと分かりますし、「5分の6」は「1を5等分した6個分」だから1より大きくなると理解できます。
「1」をもとにしていることに意識を向けることで理解が深まり、4年生で習う帯分数や仮分数などにも繋がっていくのです。
分数の計算
分数の計算をお子さんに理解してもらうには工夫が必要です。
計算方法だけ覚えることは訓練すれば出来ます。
「分母は足さずに分子を足すだけ」とこれを忘れなければ正しい答えは求められます。
ただ、なぜそうなるかを理解することはなかなか難しいものです。
理解のためにやはり「もとにして」という考え方を意識して教えてあげましょう。
「5分の4」は「5分の1をもとにしてその4個分」と言うこともできます。
そうなりますと、「5分の4」-「5分の2」の計算は「5分の1」をもとにするので「4-2」の計算で考えられるのです。
分母が10であれば、「10分の1」や「0.1」をもとにしても計算を考えることができますね。
確かに「分数」は3年生のお子さんたちが理解するには難しい章ですが、「もとにして」という考え方を丁寧に確認しながら学んでいけばきちんと理解してくれるでしょう。
![]() 無料算数学習プリント
無料算数学習プリント
ふたば問題集
小学3年生 第15章「分数」