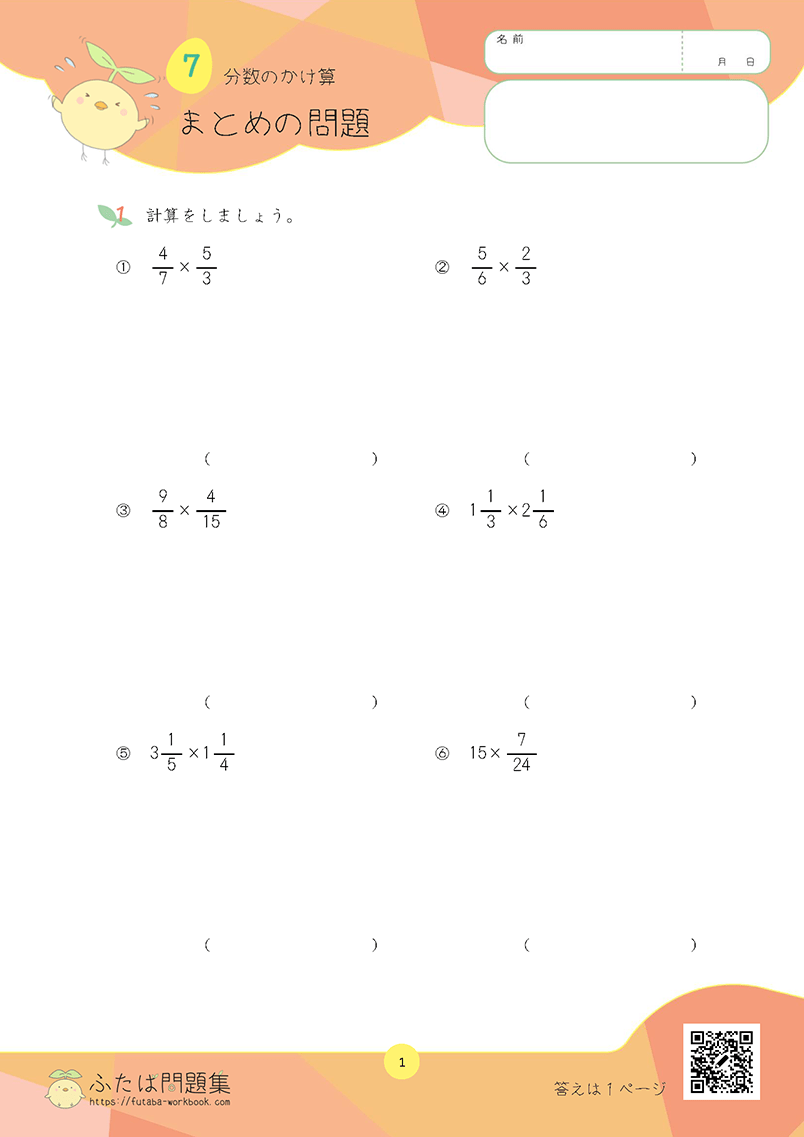言葉の意味を理解しましょう。
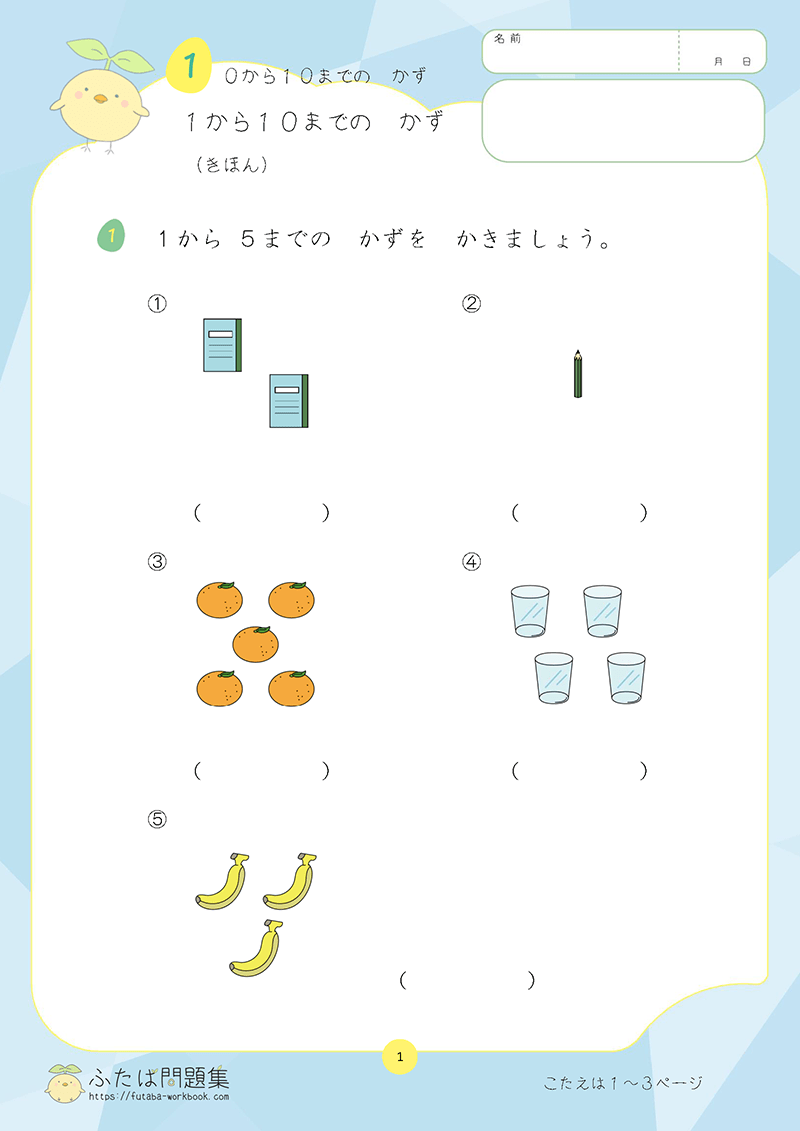
小学3年生の第8章「あまりのあるわり算」です。
この章では「わりきれる」、「わりきれない」、「あまり」という3つの言葉の意味を理解することが大切です。
今までの学習で行ってきたのは「あまりのないわり算」でした。
この「あまりのないわり算」は、「わりきれる」ということだったことを教えてあげてください。
また「わりきれない」と「あまり」を教える際に、例えばこんなことをしてみましょう。
お子さんと「2人で5個のあめ」を分けてみます。
すると1人2つずつもらったところで、あめが1つ残りますね。
この場合のわり算を式で考えると、
「 5÷2=2あまり1」
です。
この残った1つのあめのことを「あまり」と呼び、あまりがあるので「わりきれない」ということを教えてあげてください。
「あまりのある割り算」の解き方のコツ
「あまりのないわり算」を解く時は、割られる数を九九の答えから探して答えを出すことができました。
しかし「あまりのある割り算」では、割られる数が九九の答えにありません。
代わりに割られる数に近い九九の答えを探すことで答えを予想する必要があります。
例えば「13÷3」という問題を考えてみましょう。
13に1番近い3の段の九九の答えの数は、「3×4=12」なので12です。
そこから、「13÷3=4あまり1」と求めることができます。
このように九九の答えを活用して割り算の答えの見当をつけることができます。
この方法では、割られる数に近い九九の答えを探しますが、九九の答えより割られる数が大きくなければいけません。
このように一つ一つ順序立てながら教えてあげてください。
何度も練習問題を解きながら「あまりのあるわり算」に慣れることが大切です。
![]() 無料算数学習プリント
無料算数学習プリント
ふたば問題集
小学3年生 第8章「あまりのあるわり算」