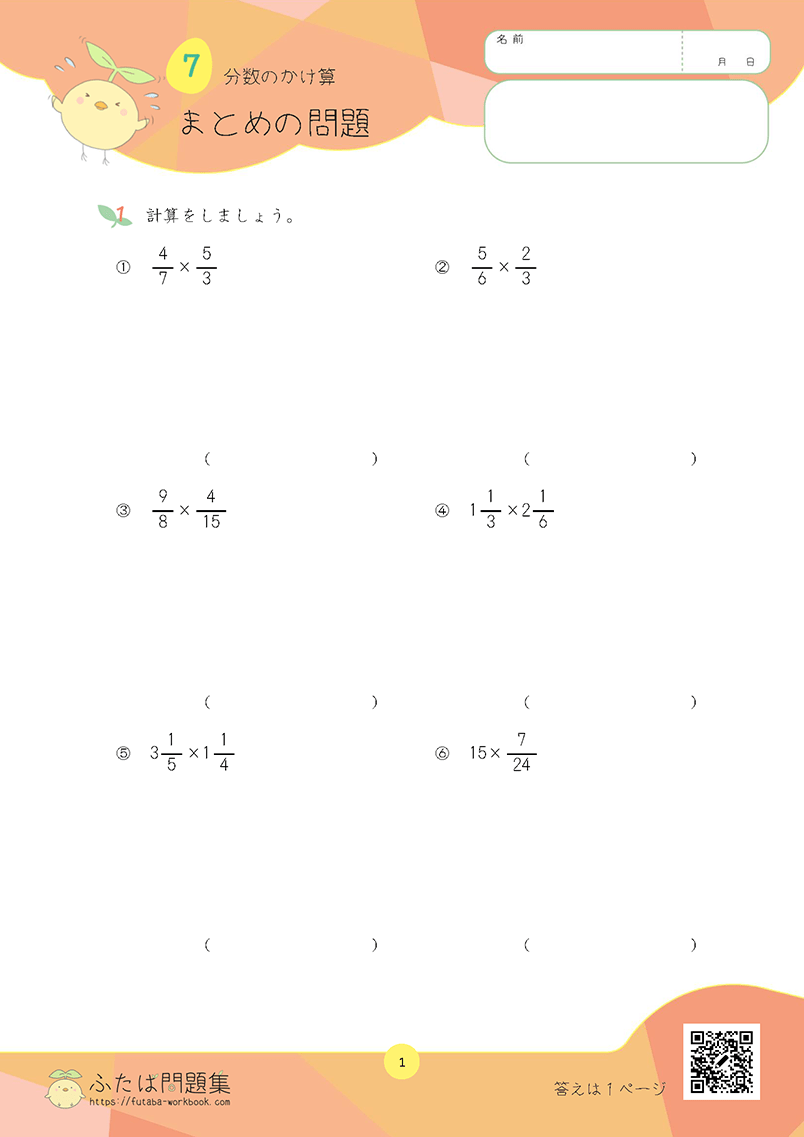わり算の筆算を求められるようにしましょう
小学4年生の第3章「わり算の筆算(1)ーわる数が1けた」では、わり算の筆算を学習します。
3年生で学習したわり算を活用しながら「2けたや3けたの数を1けたの数でわる計算」を筆算で求めます。
まずは、筆算の考え方を理解しましょう。
例えば、72÷3。
これは「(70+2)÷3」として考えます。
1.計算しやすいように、72 を70と2にわける
2.70は、10 のまとまりが7こだから、まず十の位である「7÷3=2あまり1」を計算する

3.「2あまり1」は、答えが「20(のまとまりが2こ)」、あまりが「10(10のまとまりが1)」という意味
4.あまりの「10」に、72ののこりである「2」を足す(10+2=12)

5.次に「12÷3=4」を計算する
6.「72÷3」の商は20と4を合わせた24となる。

わり算の筆算では、この考え方が土台になっています。
このように、わり算の筆算では、かけ算やわり算で学習した考え方や計算法が欠かせません。
わり算の筆算につまずいた場合は、かけ算やあまりのあるわり算を復習してみましょう。
わり算のあまりに要注意
わり算の筆算では、わりきれない場合があります。
筆算の場合、一番下にある数があまりとなります。
- あまりがない場合:一番下にある数は0
- あまりがある場合:一番下にある数は0以外

これまでとちがって、商とあまりが別々にあるため、見逃させないよう注意しましょう。
わり算の応用力も身につけよう
わり算の基本的な知識を生かして、応用問題にも挑戦しましょう。
2400÷4の場合
2400は100のまとまりの24こ分だから、「24÷4」で計算する
4こ入は12こ入の何倍かを求める場合
「12(比べられる数)」の中に「4(もとになる数)」がどれだけあるかで考えます。
そのため、式は「12÷4=3」、答えは「3倍」になります。
このように、わり算を確実に身につければ、応用問題も解けるようになるでしょう。
ここで身につけたスキルは、5年生の小数の計算や6年生の分数の計算につながります。
多くの問題を解いてわり算の筆算をマスターしましょう。
![]() 無料算数学習プリント
無料算数学習プリント
ふたば問題集
小学4年生 第3章「わり算の筆算(1)ーわる数が1けた」