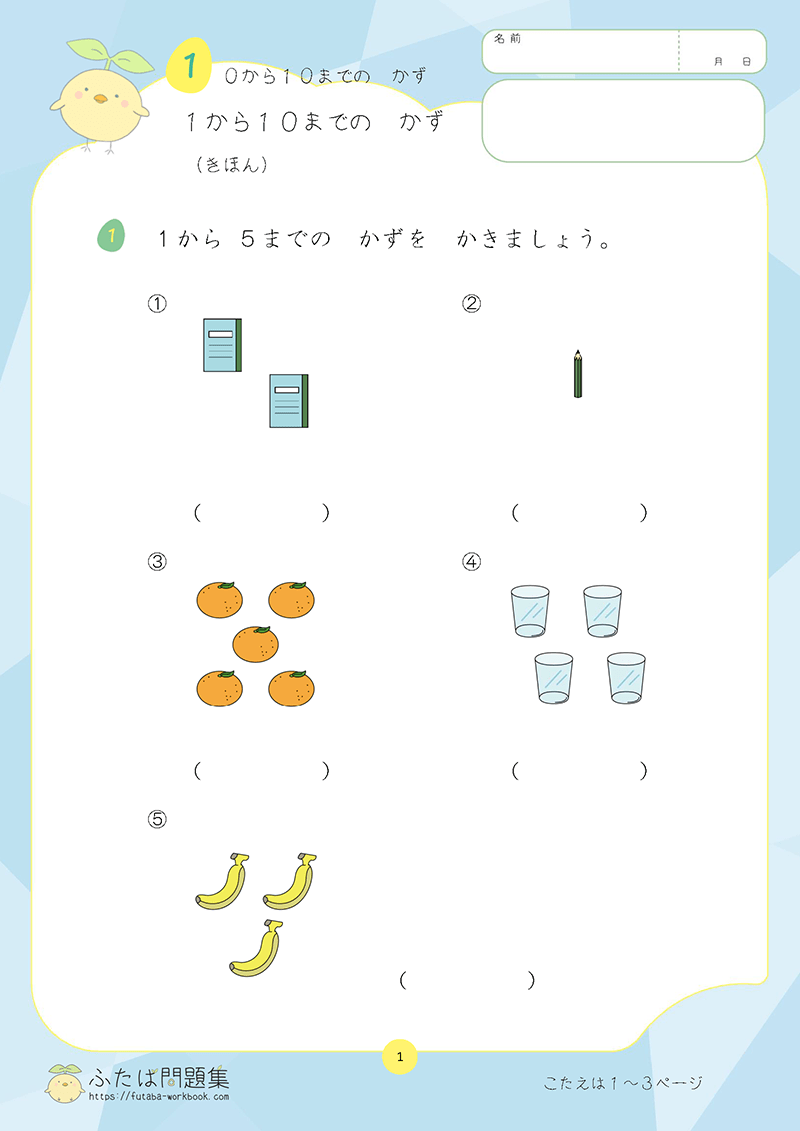
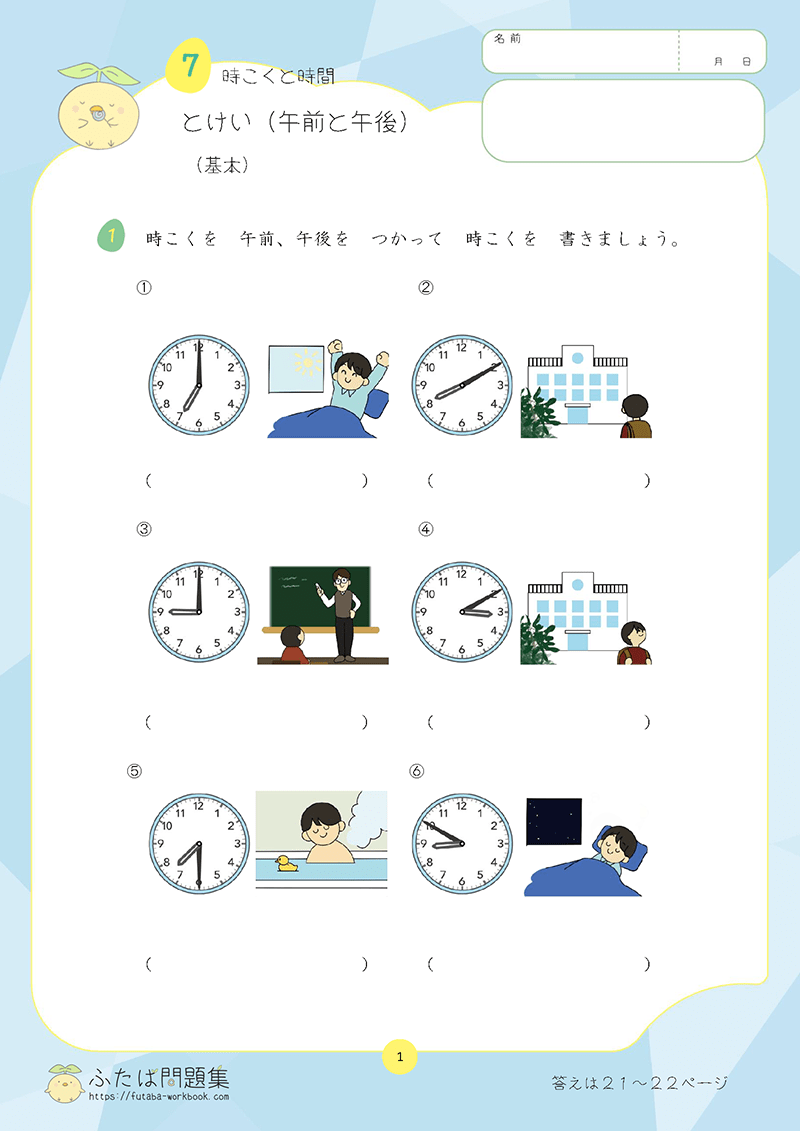
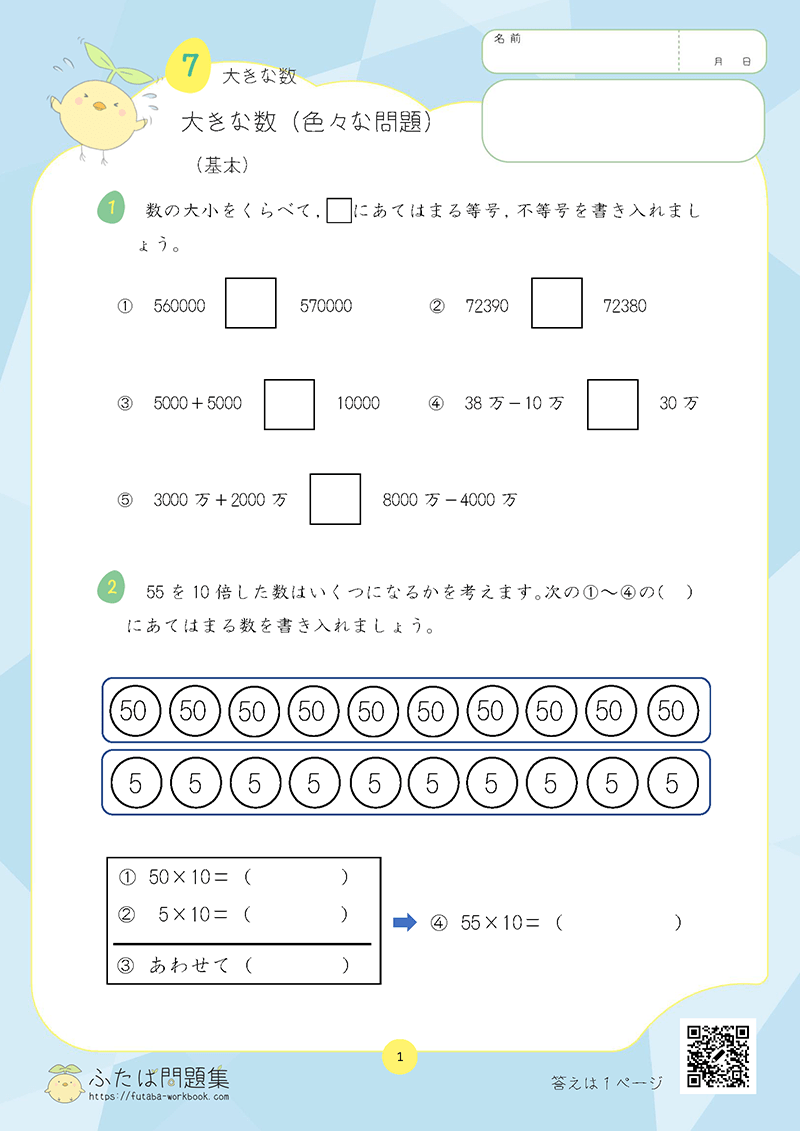
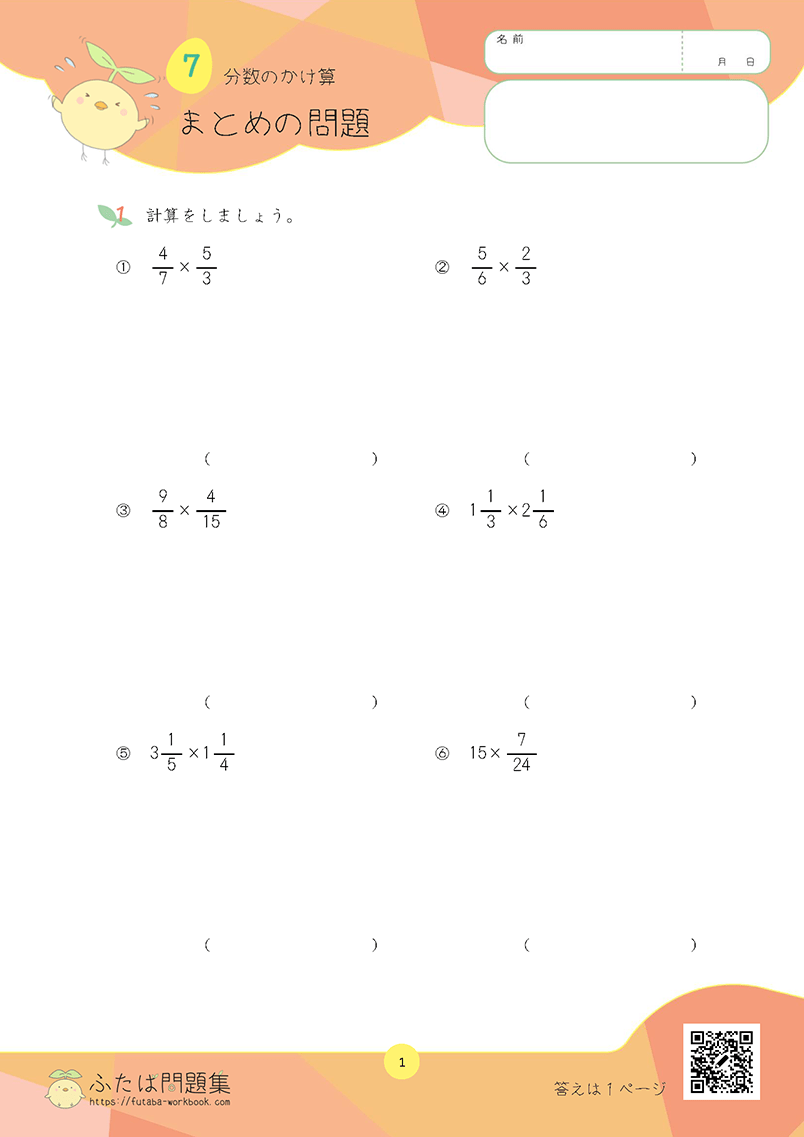わる数が2けたでもやることは同じ
小学4年生の第6章「わり算の筆算(2)ーわる数が2けた」です。
これまで、2けたや3けたの数を1けたの数でわる計算を学習しました。
この章では、わる数が2けたになる計算を学習します。
とはいえ、筆算のやり方はこれまでと変わりません。
まずは、筆算の方法をもう一度確認しましょう。
例えば、46➗12の場合
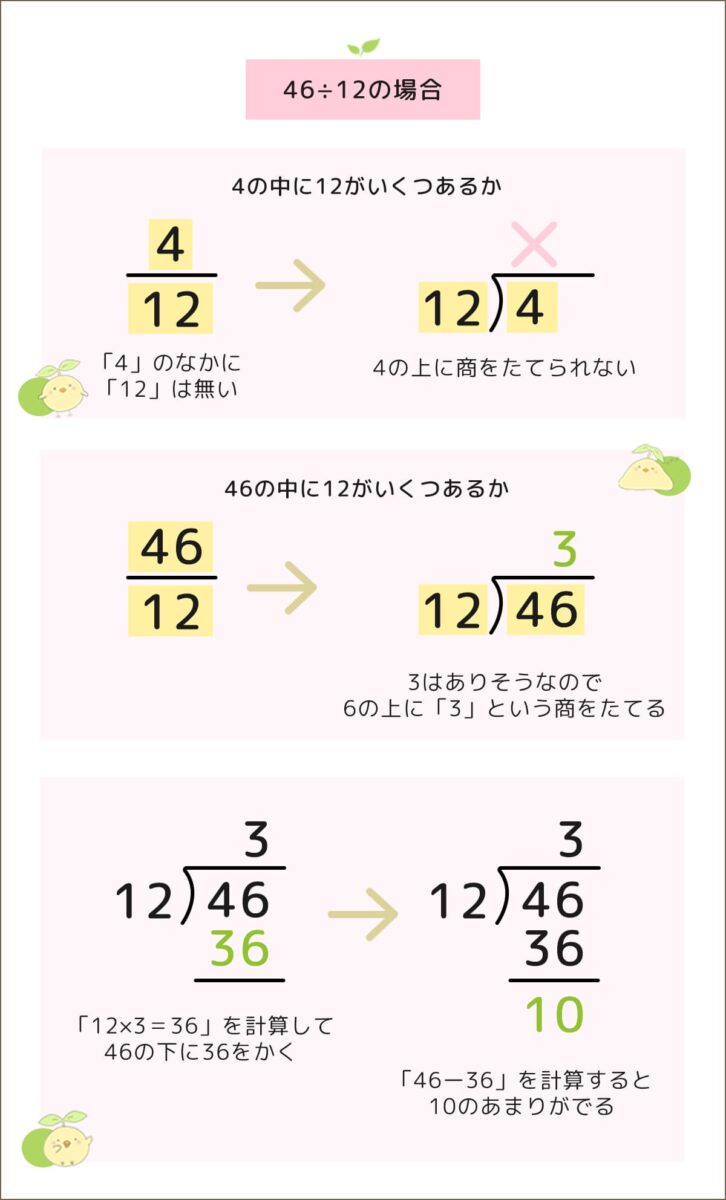
- まず、「4の中に12がいくつあるか」を考える(4➗12)
- 4の中に12はないので、4の上に商をたてられない
- 次に「46の中に12がいくつあるか」を考える(46➗12)
- 3はありそうだから、6の上に「3」という商をたてる
- 「12×3=36」を計算して、46の下に36をかく
- 「46ー36」を計算すると、10のあまりがでる
わり算の筆算は苦手意識をもつ子どもが多い内容です。
しかし、手順を正しく覚えれば、スラスラ解けるようになります。
やり方が身につくまで、くり返し練習しましょう。
10や100のまとまりを活用しよう
わり算でも、10や100のまとまりを生かして計算することも大切です。
例えば、「2800➗7」で考えてみましょう。
このまま計算しても間違いではありません。
しかし、2800は100のまとまりが28こだから「28➗7」と考えた方がより簡単に計算できます。
算数では、早く簡単に解くことも求められています。
10や100のまとまりで考えるのがむずかしい場合、「2800円は百円玉何個分かな?」
など、お金に置き換えて考えるのがおすすめです。
わり算の性質を理解しよう
わり算の性質を理解し、計算に活用する力も大切です。
例えば、15➗5=□➗30の場合。
パッと見ると「2つのわり算を解かなければいけないから大変そう」と感じますよね。
しかし、わり算の性質を利用すれば簡単に解けます。
その性質とは「わられる数」と「わる数」に同じ数をかけて計算しても、答えは同じになることです。
では、もう一度「15➗5=□➗30」をみてみましょう。

- 「15➗5」と「□➗30」は答えが同じになる
- わる数に注目する。「5」を6倍すると「30」になる
- わられる数の「15」も6倍すれば「□」がわかる
このように、わり算の性質を理解し活用できるようになることも大切です。
ここで身につけたスキルは、5年生の小数の計算や6年生の分数の計算につながります。
多くの問題を解いてわり算の筆算や性質をしっかり理解しましょう。
![]() 無料算数学習プリント
無料算数学習プリント
ふたば問題集
小学4年生 第6章「わり算の筆算(2)ーわる数が2けた」