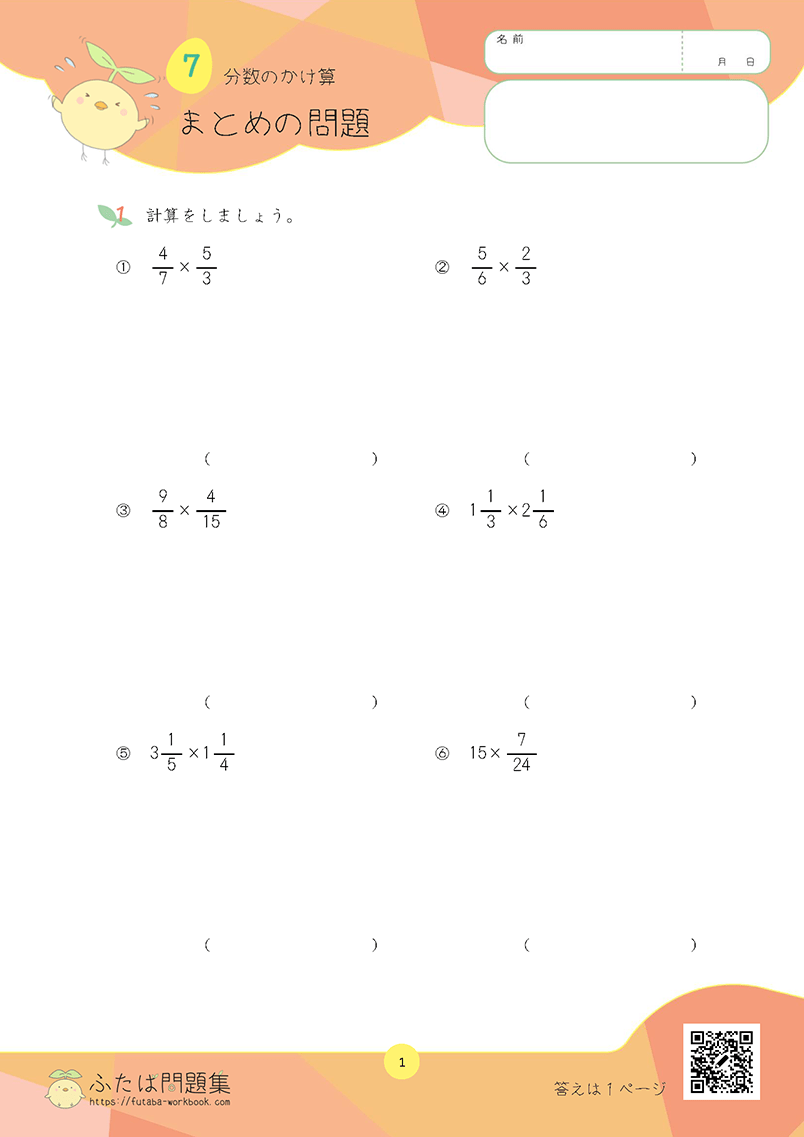「ひっ算の準備」が大切です
「たし算のひっ算（２けた）」は、初めて筆算の計算方法を学ぶ単元です。
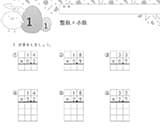
23＋6の問題は、「23は十のまとまりが2個と、ばらが3枚」「6は十のまとまりは0個で、ばらが6枚」と分かるでしょうか。
「ばら」とは「一がいくつ分」ということです。問題集では「ばらが3枚」と表現しています。
しかし、十のまとまりの方は、シールの枚数ではなく十のまとまりの数と捉えて、2枚ではなく「十のまとまりが2個」となっています。
タイルで教える場合は、まとまりの数え方を百のタイルは1枚、十のタイルは1本、一のタイルは1個と数え方の単位を変えてイメージしやすくする方法もあります。
最終的に、図や絵がなくても2桁の数字を見ただけで、「十のまとまりが□個とばら（一）が□（個）」と分かるようになることが大切です。
それが、十の位と一の位を分けて計算する筆算の計算方法に繋がります。
「ひっ算ってなに？」子供はその意味を知りません
筆算と式は違います。
文章問題で筆算だけ書いても正解にはなりません。
文章問題では基本的に「式と式の答え」と「問題の答え」を書きます。
筆算は「式の答えを出すための計算」なのです。
右側はばら（一）が入る部屋で、左側は十のまとまりが入る部屋です
3＋38の問題では、3を十の位に書いてしまう間違いが多いので気をつけましょう。
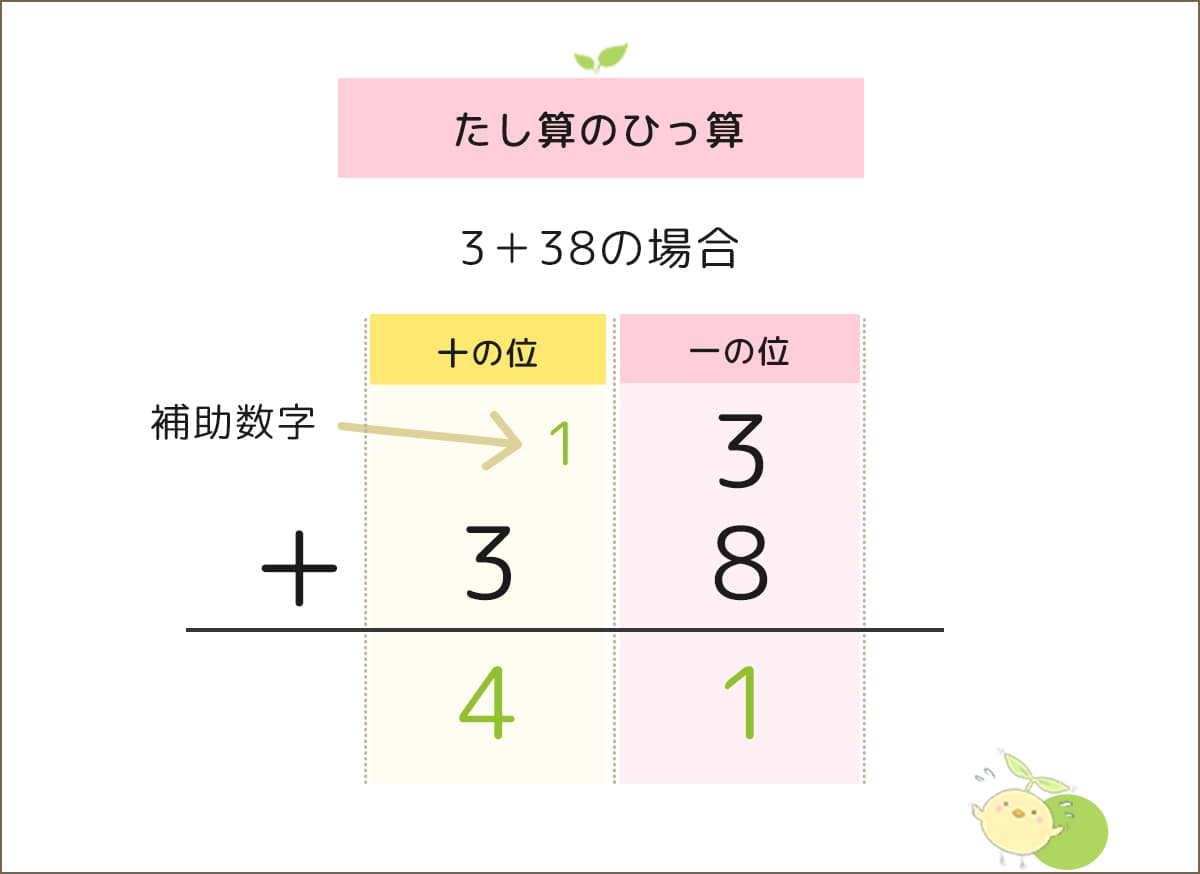
繰り上がりのあるたし算の筆算では、補助数字を書き込みます。
どこに書かせるか様々な方法がありますが、十の位の縦の範囲内に書かせましょう。
一の位に10だった数は十の位では1の数字に変わるので、例えば十の位の数字の上に補助数字1を書き込むことで筆算の助けになります。
