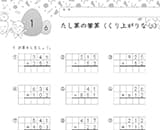
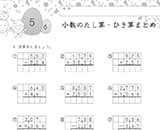
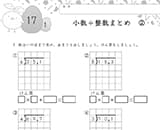
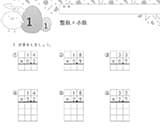
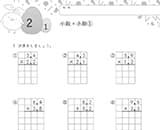
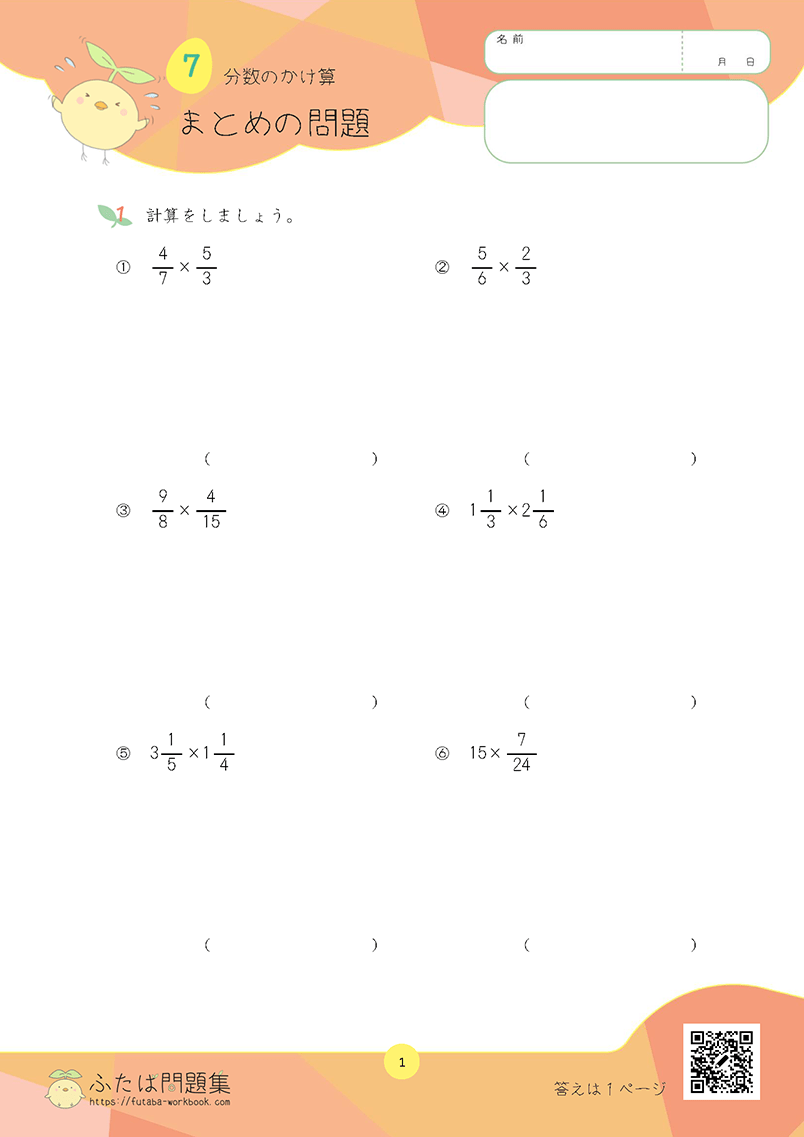1桁や2桁の計算で学んだことを生かしましょう
小学2年生の第9章「たし算とひき算のひっ算」は「3桁の計算」を学習する単元です。
「3桁の計算」は「1桁や2桁の計算」を活用すれば答えが出せることを学びます。
この学習でつまずいた場合は、1桁や2桁の計算をもう一度丁寧に復習してみましょう。
「3桁の計算」は「1桁や2桁の計算」を活用しよう
3桁の数字を見ると「難しそう」「自分には無理かも」と思うお子さんもいるかもしれません。
けれど、たし算のひっ算も、ひき算のひっ算も計算方法は1桁や2桁の計算ができれば、解ける問題ばかりです。
「これまでと同じように解けば、大丈夫」と励ましの言葉をかけてあげてください。

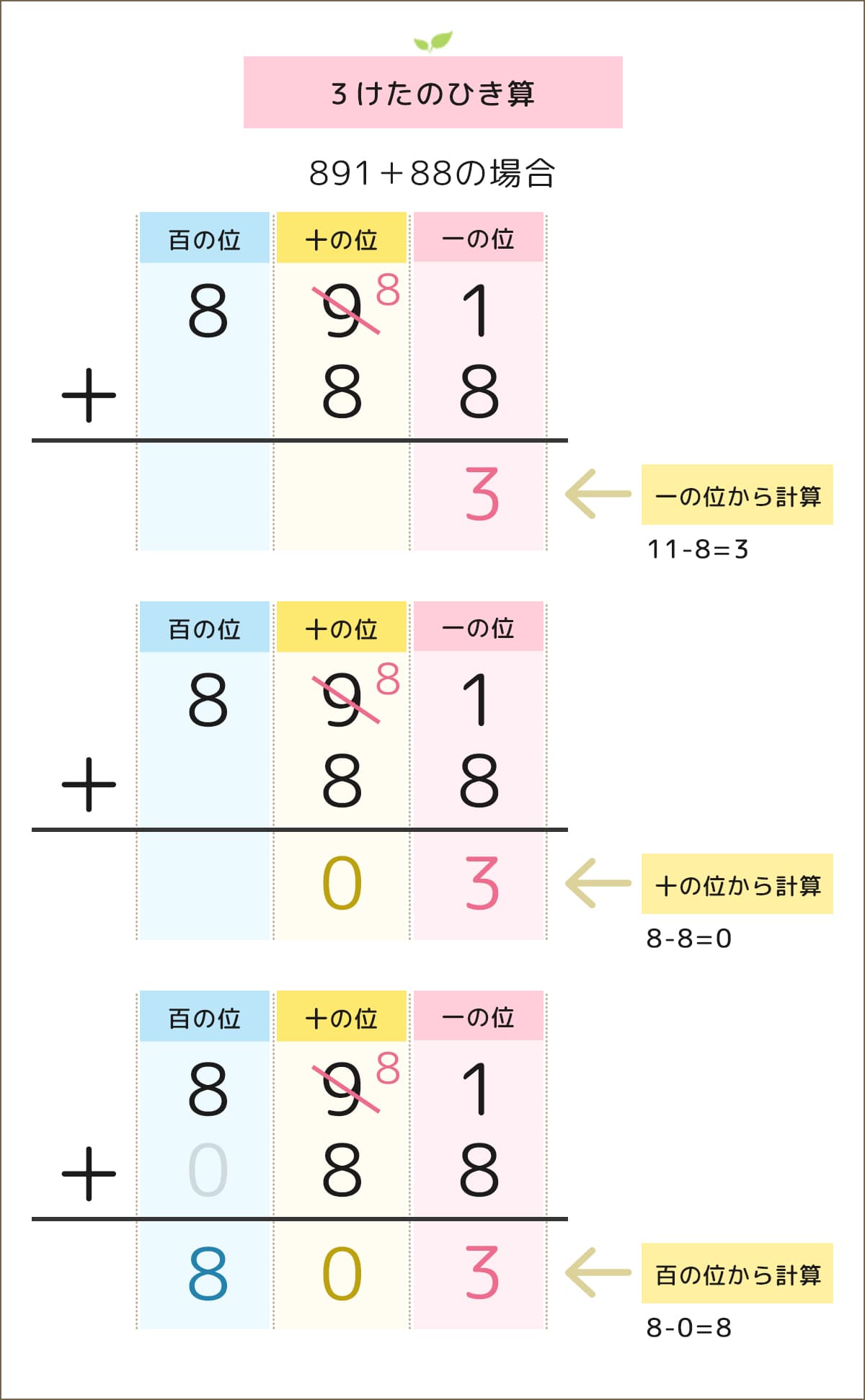
3桁の計算は練習あるのみです
問題や答えに3桁以上の数がある場合、答えまでの計算タスクが増える分、間違いが多くなります。
例えば、足し算で1回の繰り上げがある問題はきちんとできてもそれが2回必要になると、十や百の位に繰り上がった「1を足し忘れ」てしまうミスが多く起こるのです。
これは引き算の繰り下がりでも同様です。
一の位、十の位、百の位など、それぞれの数のまとまりを理解するのがむずかしい場合は、お金など、具体物を使うとより理解しやすくなります。
お金やスーパーでの買い物など、身の回りのものをうまく活用しながら、何度も問題を解いて計算力アップを目指しましょう。
![]() 無料算数学習プリント
無料算数学習プリント
ふたば問題集
小学2年生 第9章「たし算とひき算のひっ算」