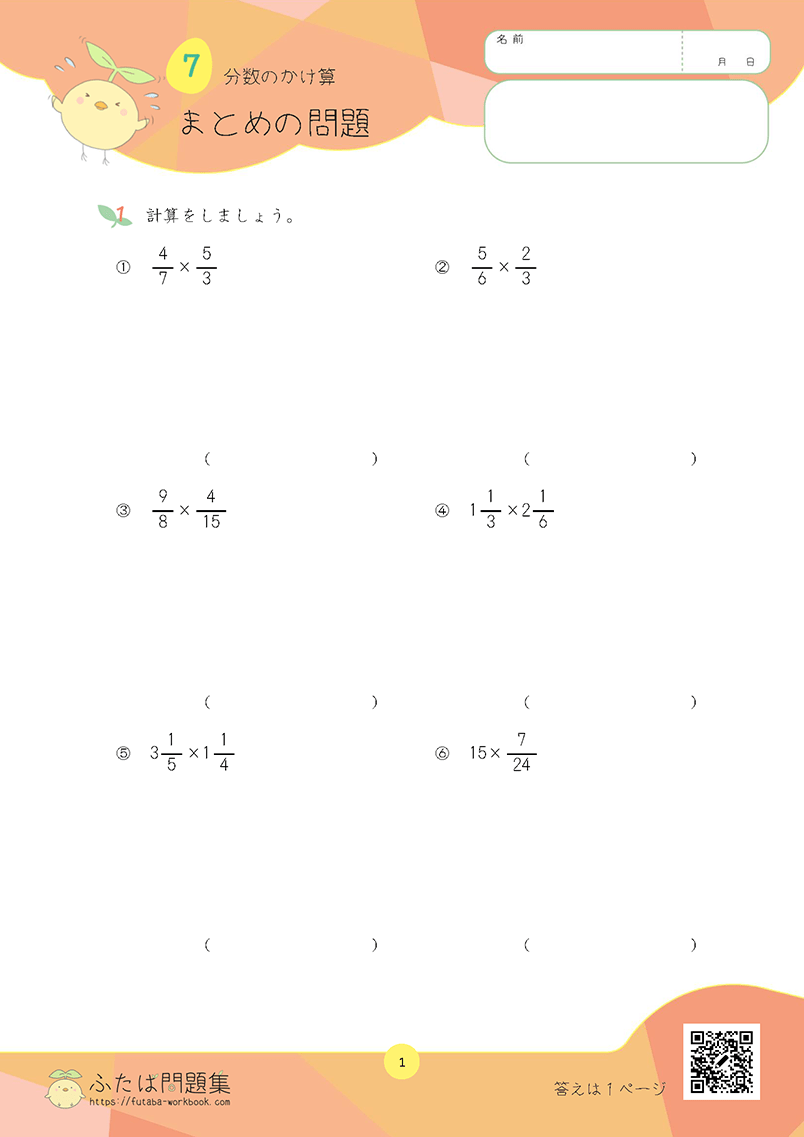小学校5年生の算数は、6年生の土台となる重要な内容が盛りだくさん。
けれども「どこから手をつけたらいいのかわからない」「短期間で効率よく復習したい」と悩む方も多いのではないでしょうか。
今回は、7日間で完了できる無料版の算数復習法をご紹介します。
無料で使える教材や工夫を取り入れた学習法で、楽しく算数力をアップさせましょう。
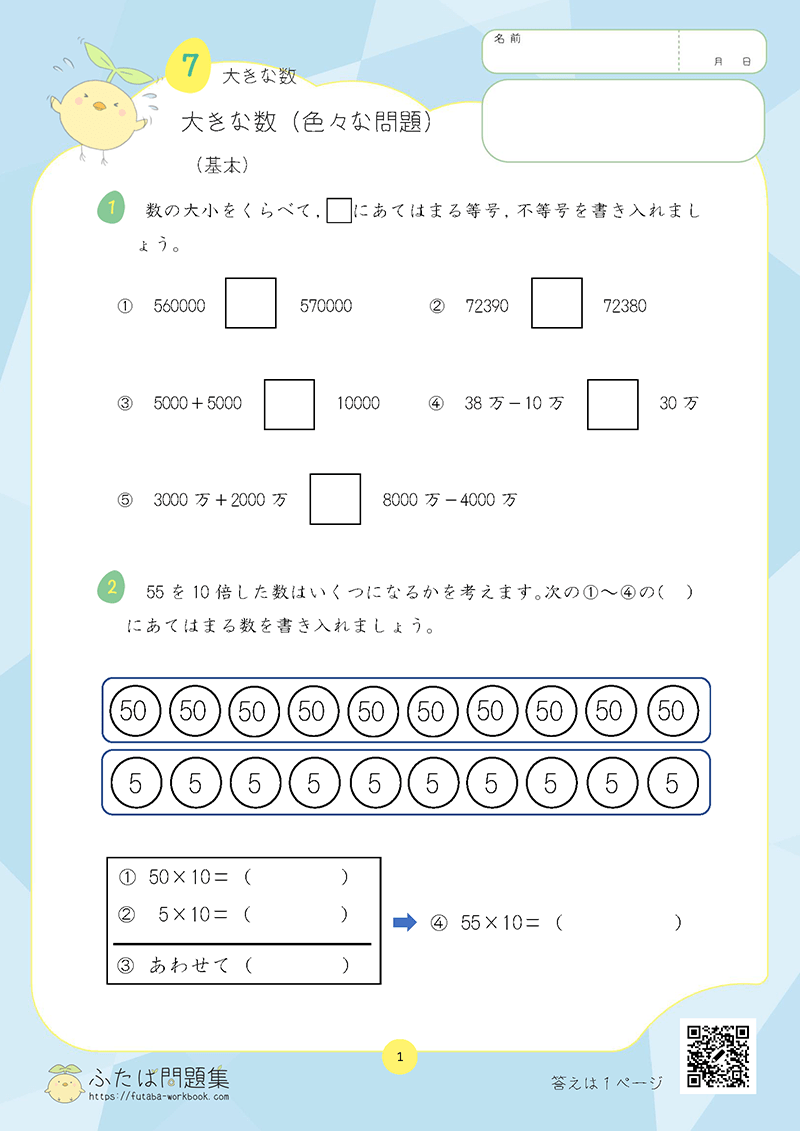
1日目:偶数と奇数、倍数と約数
まずは「偶数と奇数」「倍数と約数」の学習内容を覚えているか、理解度テストをしてみましょう。
①理解チェックリスト
- 偶数と奇数の違いを説明できる
- 12の約数をすべて言える(答え:12の約数は1、2、3、4、6、12)
- 6と8の最小公倍数と最大公約数を計算できる(答え:6と8の最小公倍数は24、最大公約数は2)
「すべてできないからダメ」「できない項目があったから算数ができない」というわけではありません。
大切なのは、占いや心理テストのように、今の自分を客観的に理解することです。
「苦手発見は点数アップのチャンス」と捉えて、前向きに取り組みましょう。
②プリントを活用して、理解を深めよう
倍数と約数がしっかり理解できると「分数の約分(分母と分子を共通の約数で割る操作)」もスムーズにできるようになります。
プリントでしっかり復習しておきましょう。
もっとくわしく解説してほしい方は、こちらも動画を活用してください。
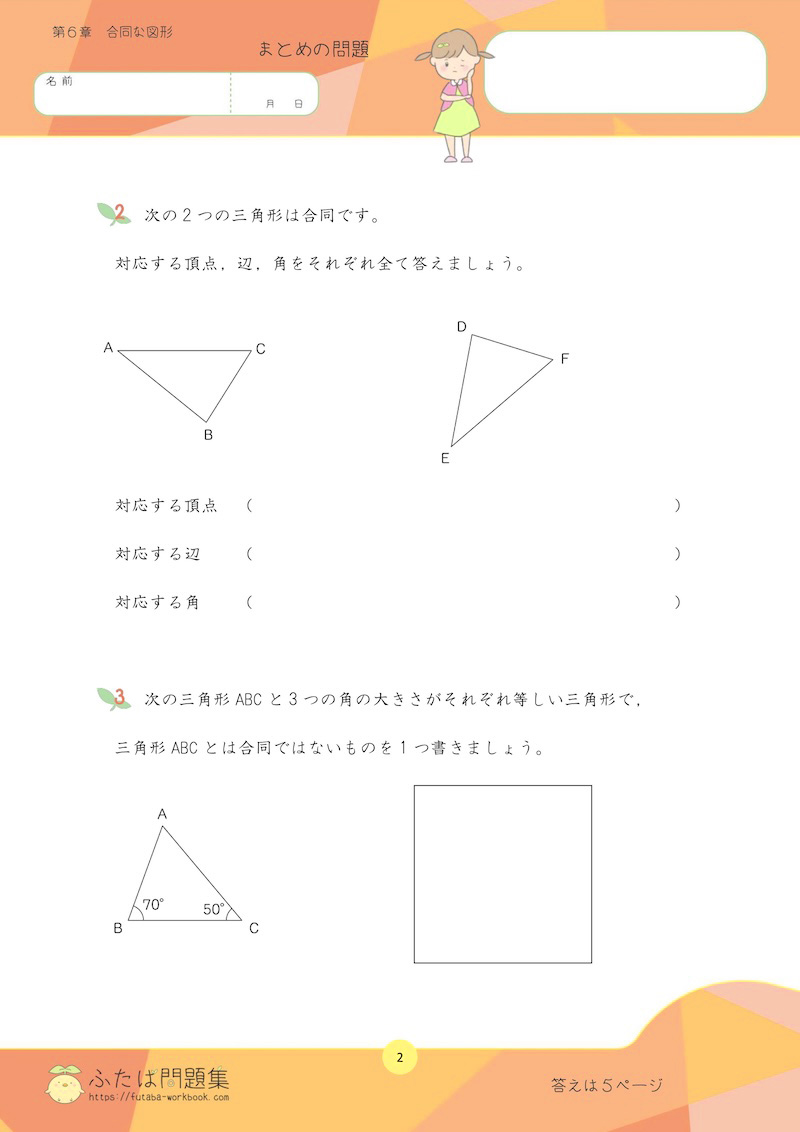
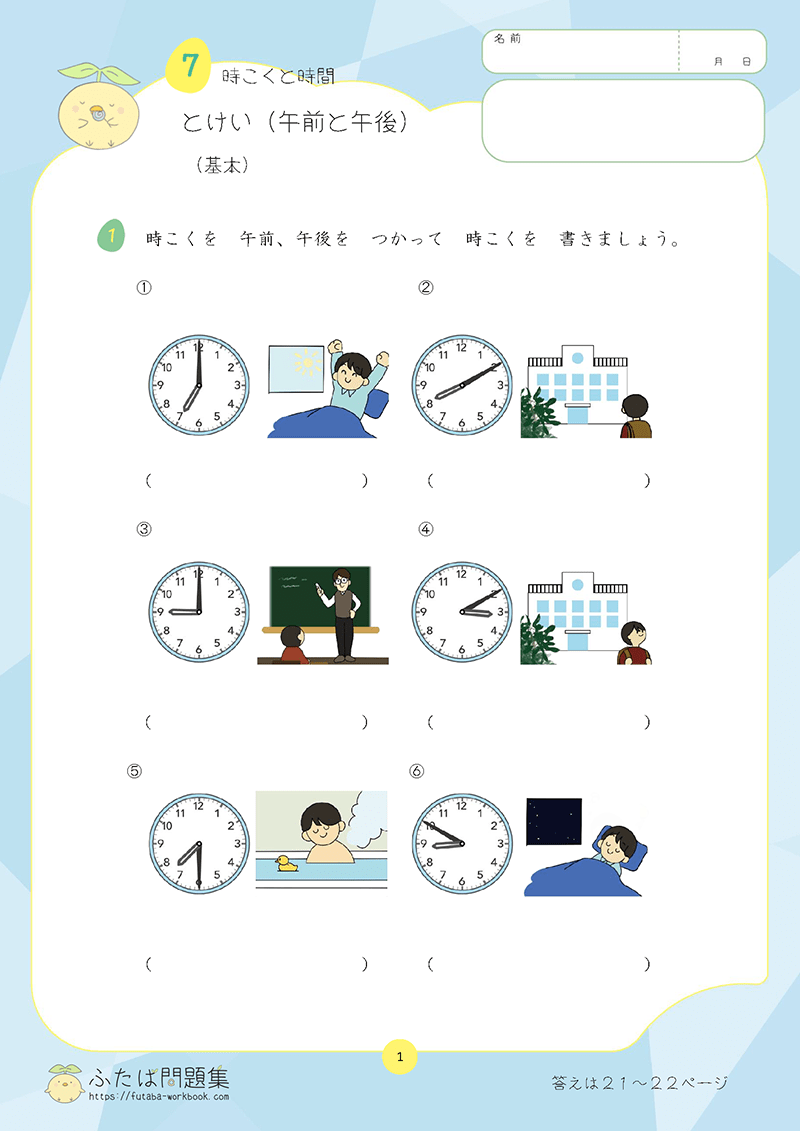
2日目:合同な図形
5年生で学習する合同な図形は、6年生の「縮図や拡大図」「対称な図形」の基礎となります。
小学6年生の算数は「対称な図形」からはじまるため、合同の概念をしっかりと理解しておくことが大切です。
①理解チェックリスト
- 合同の意味を説明できるか
「二つの図形がぴったりと重なる」「形も大きさも同じである」「対応する辺の長さや角の大きさが等しい」など、自分の言葉で説明できるか確認しましょう。
②合同な図形の理解を深めよう
「ぴったり重ねる」という具体的な操作がなくても、合同であることを判断できるように復習しましょう。
「対応する頂点、辺、角」をしっかり見極めることがポイントです。
もっとくわしく解説してほしい方は、こちらも動画を活用してください。
3日目:比例の理解
5年生の「比例」は、6年生で学習する比例の関係の基礎となるため、しっかりと理解しておくことが大切です。
①理解チェックリスト
- 日常生活で役立つ、比例の例を一つでも説明できるか
(例:買い物で商品の値段と個数の関係から合計金額を計算する、料理のときに材料の分量と人数の関係から必要な材料の量を計算する、走行距離と時間など)
「一方が変化するともう一方も変化する二つの数量」を見つけられるかがポイントです。
②表から比例の関係を読み取ろう
表を用いて表現した比例の関係から、変化や対応の特徴を読み取る力を高めましょう。
ここでは「一方が2倍、3倍…になると、もう一方も2倍、3倍…になる」といった変化の特徴を調べ、その関係性を式で表す力が求められています。
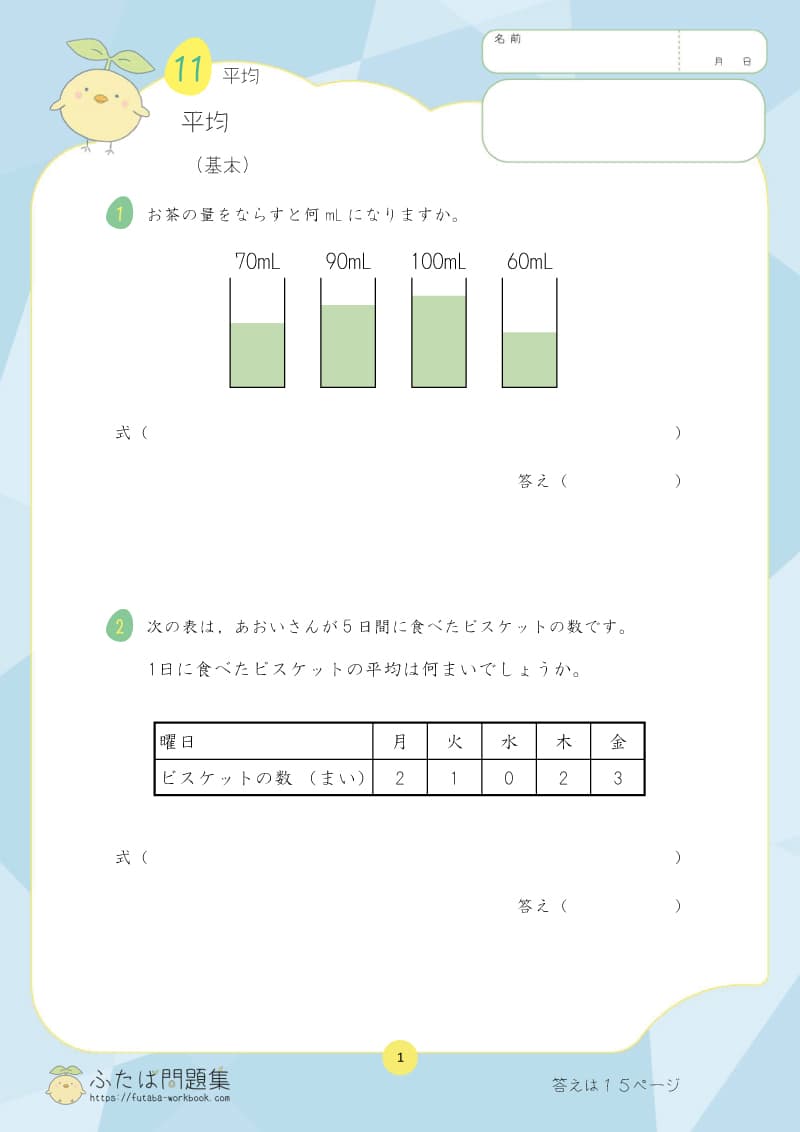
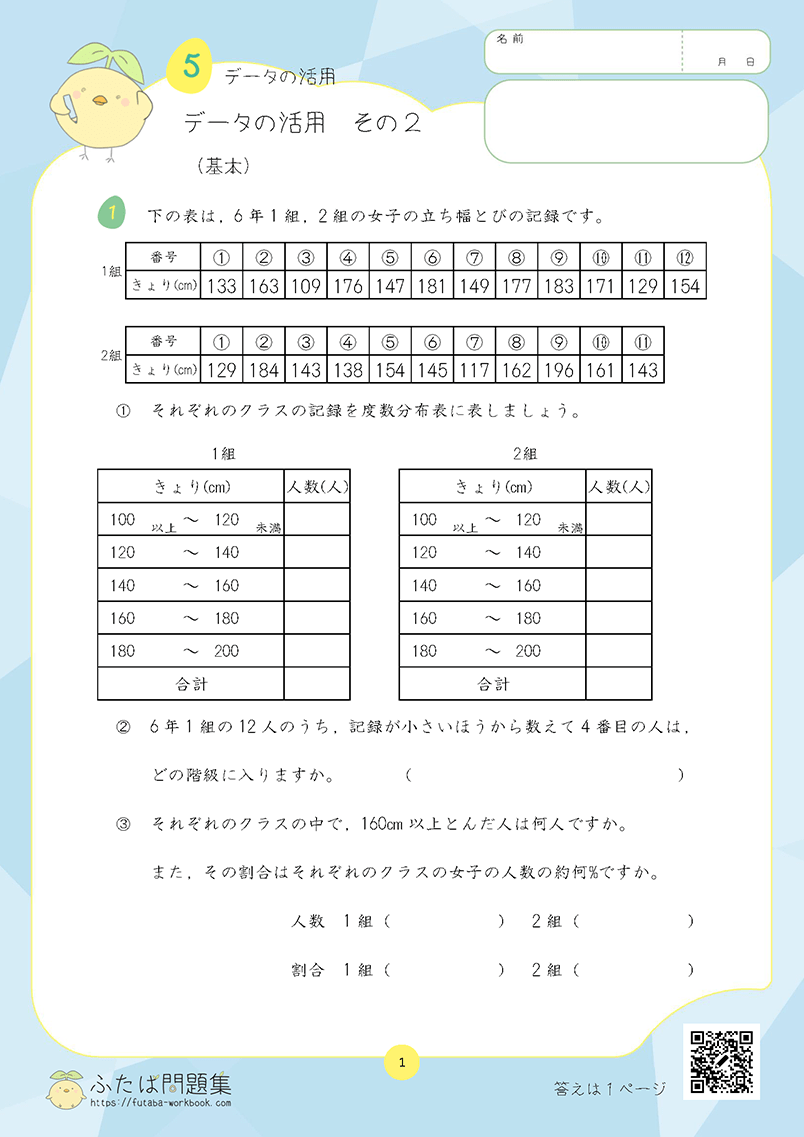
4日目:平均の求め方
平均の学習は、データを分析するために欠かせません。
例えば、自分の算数テストの平均点を出すことで、5年生での理解度がどれくらいかを数字で表せます。
このように、平均値を用いることで、大量のデータの中から全体的な傾向を把握しやすくなります。
①理解チェックリスト
- 平均の求め方(すべての値を足し合わせ、それをデータの数で等分すること)を説明できるか
完璧な答えではなくても大丈夫です。
自分の言葉で説明できるよう練習してみましょう。
②平均の求め方を復習しよう
プリントを活用しながら、計算練習をしましょう。
計算が苦手な場合は、好きなスポーツ選手の平均成績を調べたり、家族の年齢の平均を求めたりするのもおすすめです。
興味がもてる問題をくり返して、計算力を向上させましょう。
もっとくわしく解説してほしい方は、こちらも動画を活用してください。
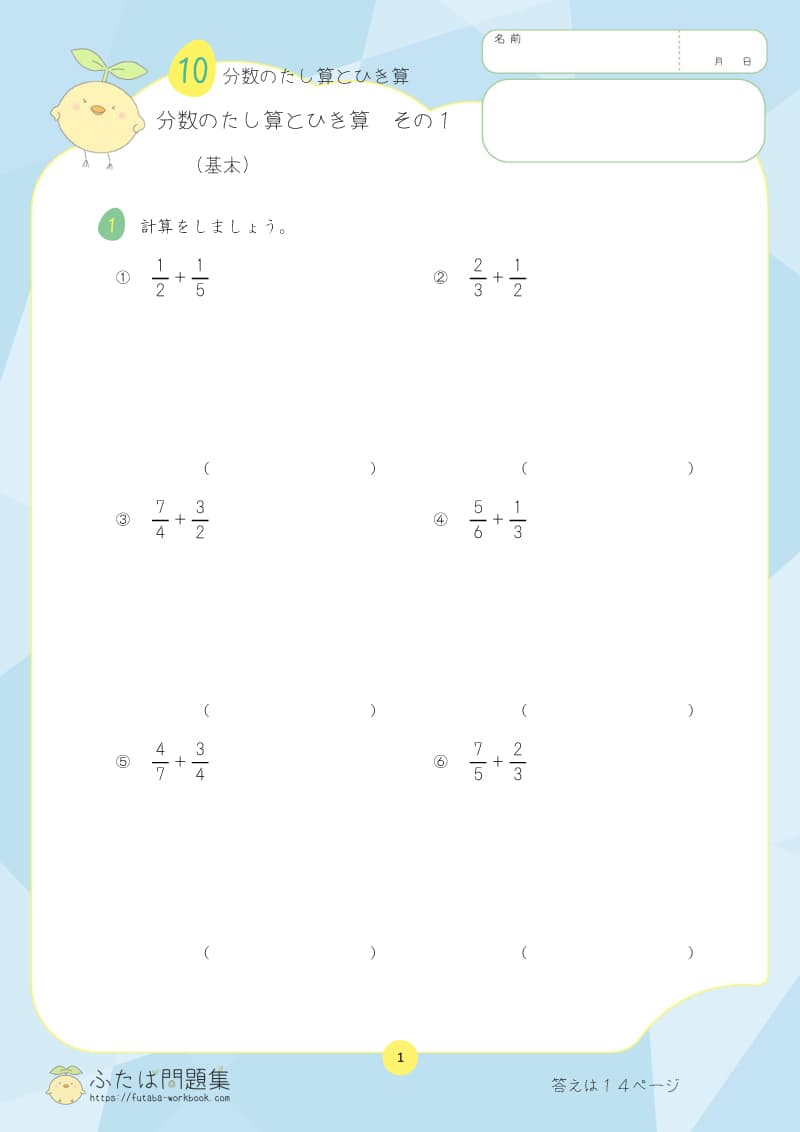
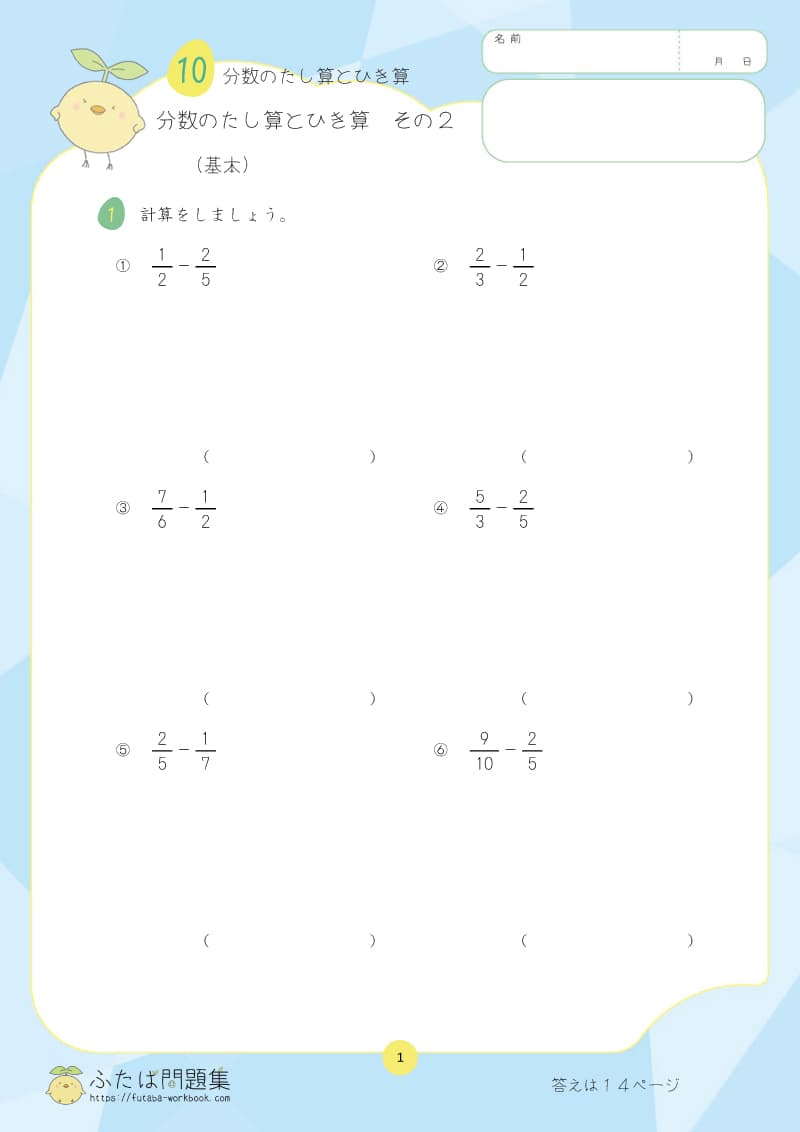
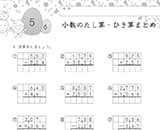
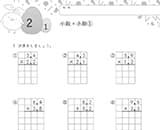
5日目:分数の計算
5年生では、分母の異なる分数のたし算・ひき算を学習しました。
ここでの学習は、6年生の「分数のかけ算・わり算」の基礎となるため、しっかり復習しておきましょう。
つまずいたら3、4年生で習う「分数の計算」を復習しましょう。
①理解チェックリスト
- 分数のたし算・ひき算で分母が異なる場合、最初に何をすべきを説明できるか
- 「通分」の意味を理解しているか
(分母を揃える操作を「通分」。通分では、それぞれの分数の分母を最小公倍数にする)
「最小公倍数」でつまずく場合は、1日目で紹介したプリントをもう一度復習しましょう。
②「通分」「約分」のスキルアップを目指そう
分母が異なる分数を計算する場合、分母を揃える必要があります。
それぞれの分数の分母を最小公倍数にしてから、計算する練習をしましょう。
また、答えが約分できる場合は約分が必要です。
忘れている場合は「約分をしなくても大丈夫?」と声をかけてあげてください。
もっとくわしく解説してほしい方は、こちらも動画を活用してください。
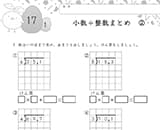
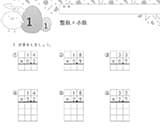
③もっと算数を復習したい方におすすめ「小数」の学習
分数と小数は、繋がりの深い内容です。
例えば、次のような例があげられます。
- 3/4を分数で表す(3÷4=0.75)
- 2/9と0.2がどちらが大きいかを考える
- 0.03を分数で表す(3/100)
また、6年生の算数には「小数」をメインとした単元はありませんが、「3,14」の円周率を使って円の面積を求めたり、データの調べ方で小数を使ったりすることがあります。
時間に余裕がある場合は、小数の計算スキルも磨いておきましょう。
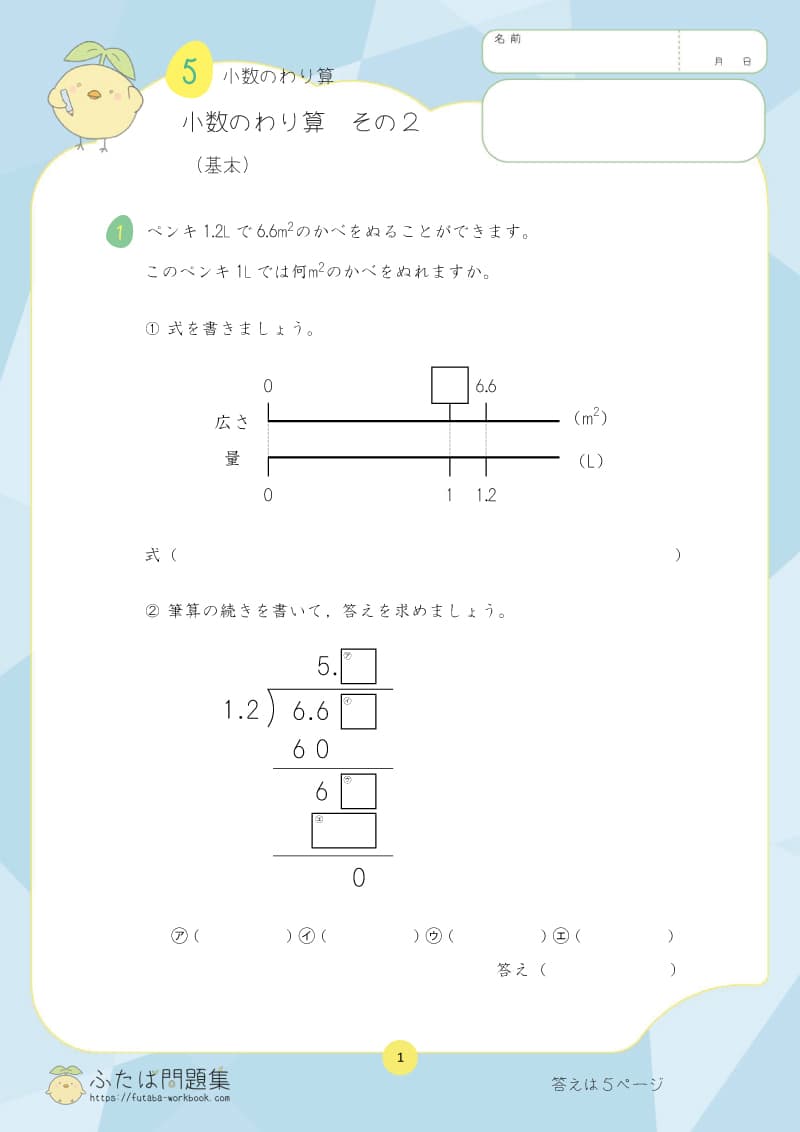
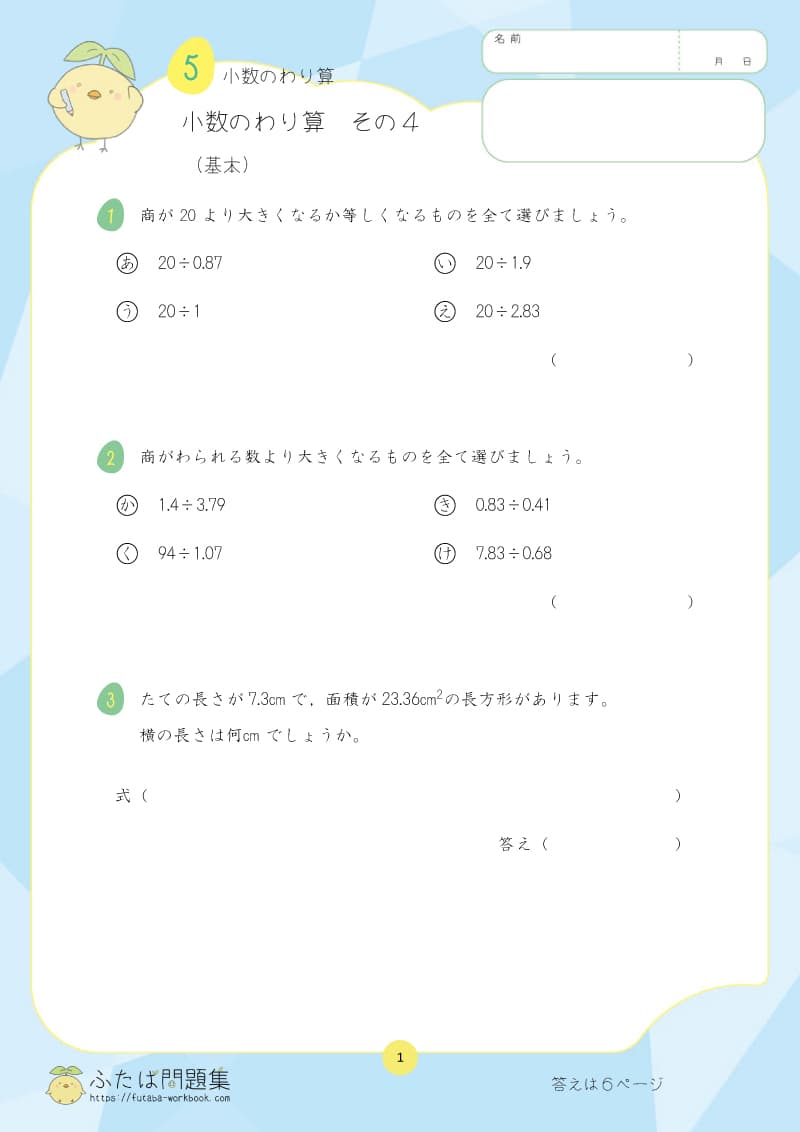
6日目:単位量あたりの大きさ
単位量当たりの大きさの意味を理解するためには、「1㎡あたりの人数や、1人あたりの面積といった、1あたりの大きさ」を考えることが大切です。
- 例1:5kmを2時間で走ったときの速さを求める。
解答:時速2.5km。
→1時間あたり2.5km進む。 - 例2:100km²に20万人が住む地域の人口密度を求める。
解答:2000人。
→1km²あたり2000人が住む。
①理解チェックリスト
- 「単位量当たりの大きさ」の具体例を一つでも説明できるか
(例:速さ、人口密度など)
ふだんの生活から、算数を意識した活動が学習意欲アップにつながります。
例えば、買い物で同じ商品でも容量や個数が違う場合、どちらがお得か一緒に考えてみましょう。
または、ドライブで車の速度と移動時間から、移動距離を計算するのもおすすめです。
②日常生活の問題を解きながら復習しよう
日常生活で起こりそうな問題の方が、イメージしやすくて考えやすくなります。
いろんな問題を解いて「単位量あたりの大きさ」の理解を深めましょう。
もっとくわしく解説してほしい方は、こちらも動画を活用してください。
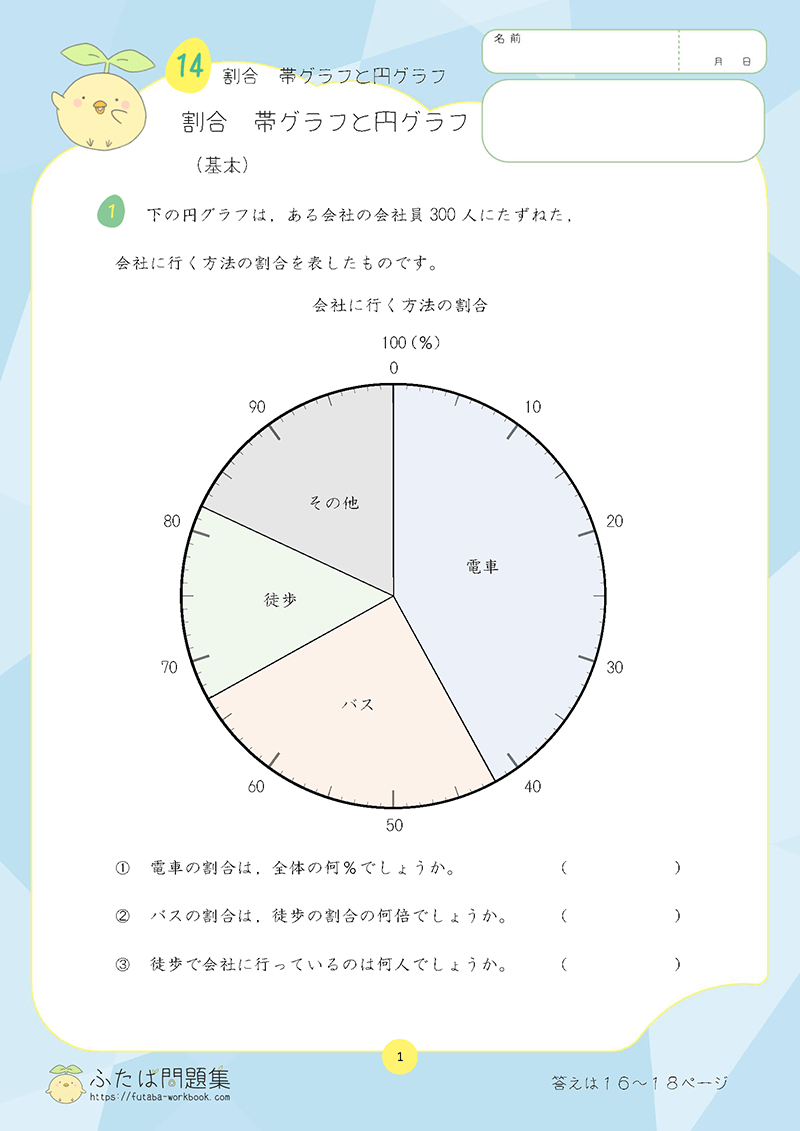
③さらに算数を復習したい方は「割合」にトライ!
「割合」は 「単位量あたりの大きさ」での学びを活かせる単元です。
「単位量あたりの大きさ」の理解を深めたい場合は「割合」を復習しましょう。
「3割引」や「乗車率120%」、「20%増量」など、日常でよく見かけるものではありますが、つまずきやすい学習でもあります。
「もとにする大きさ」と「比べられる量」を明確にしながら、問題をくり返し解いていきましょう。
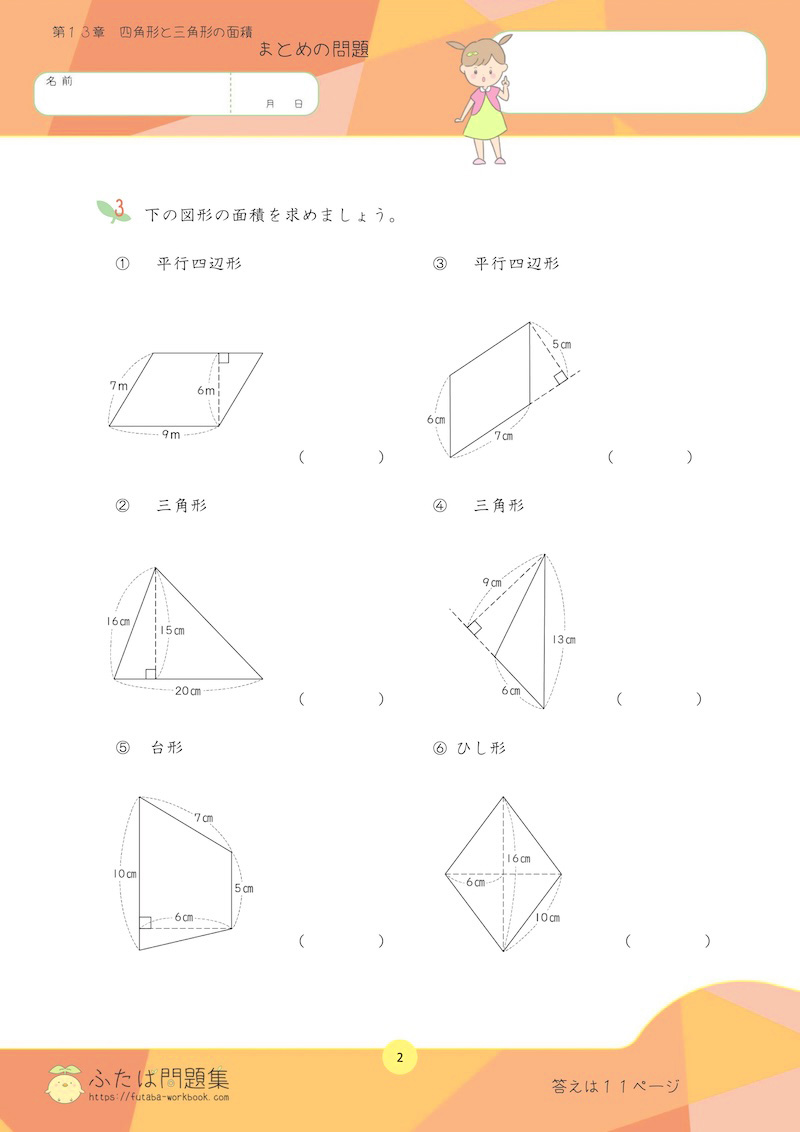
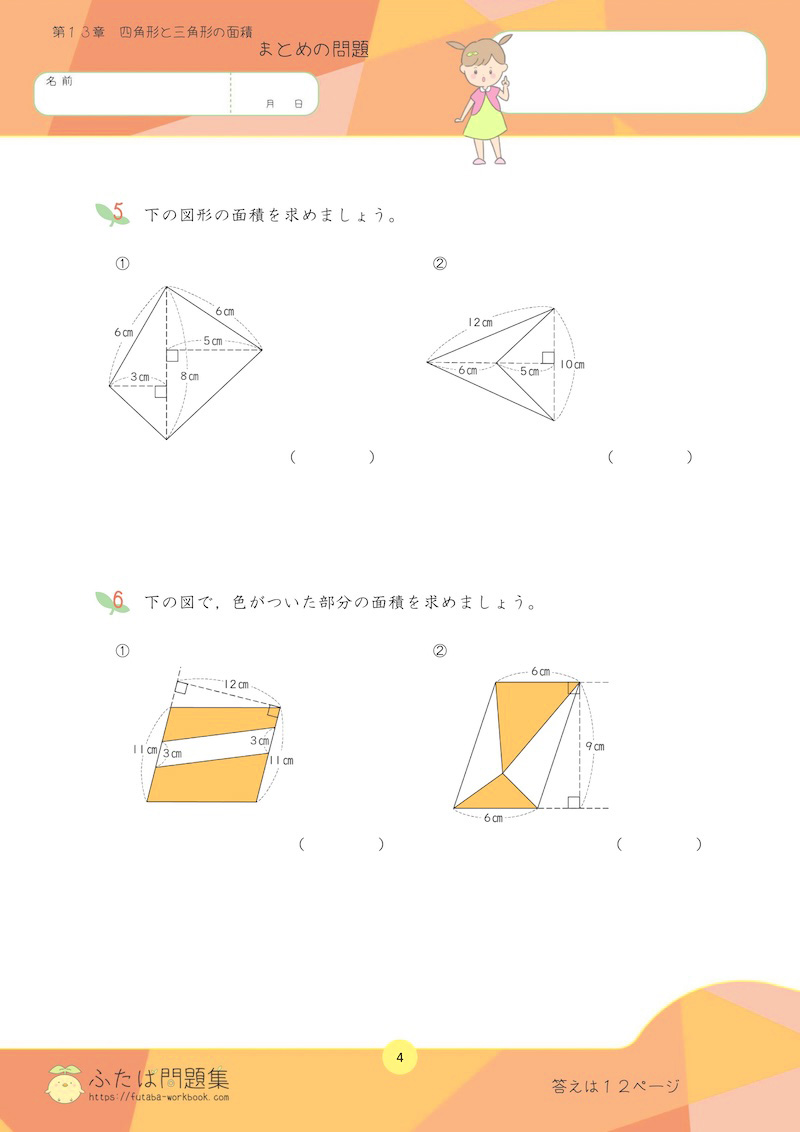
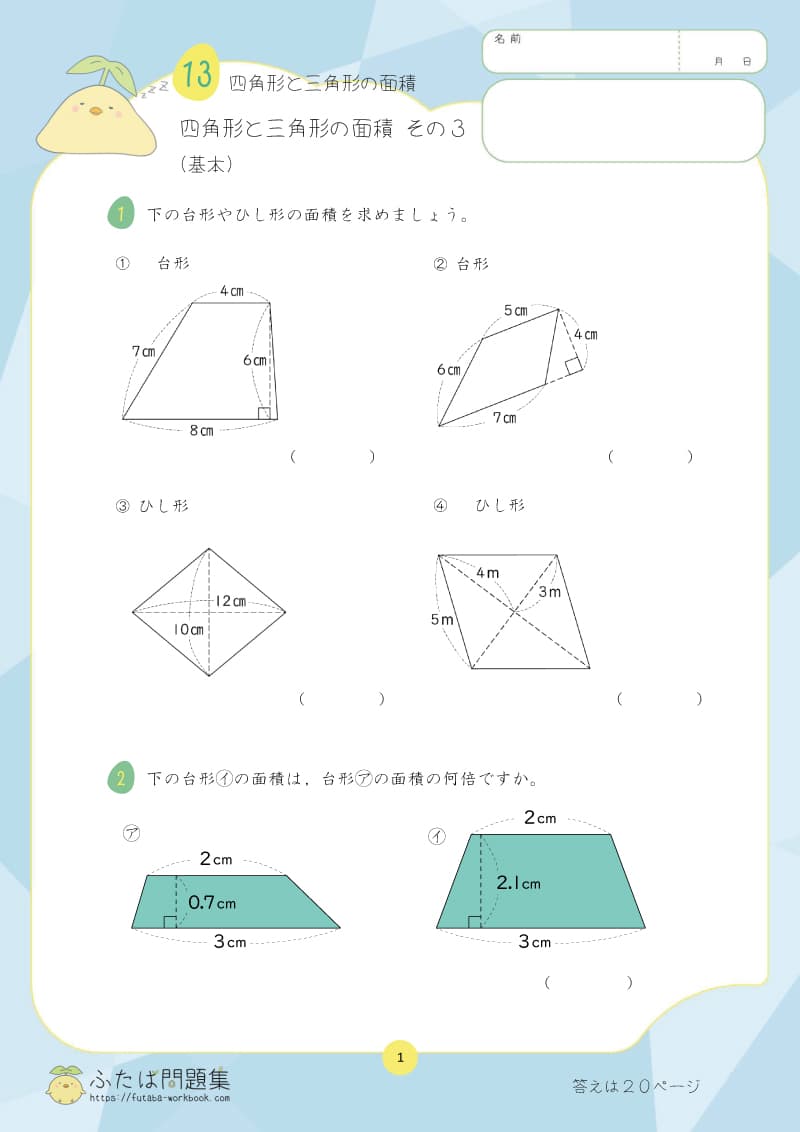
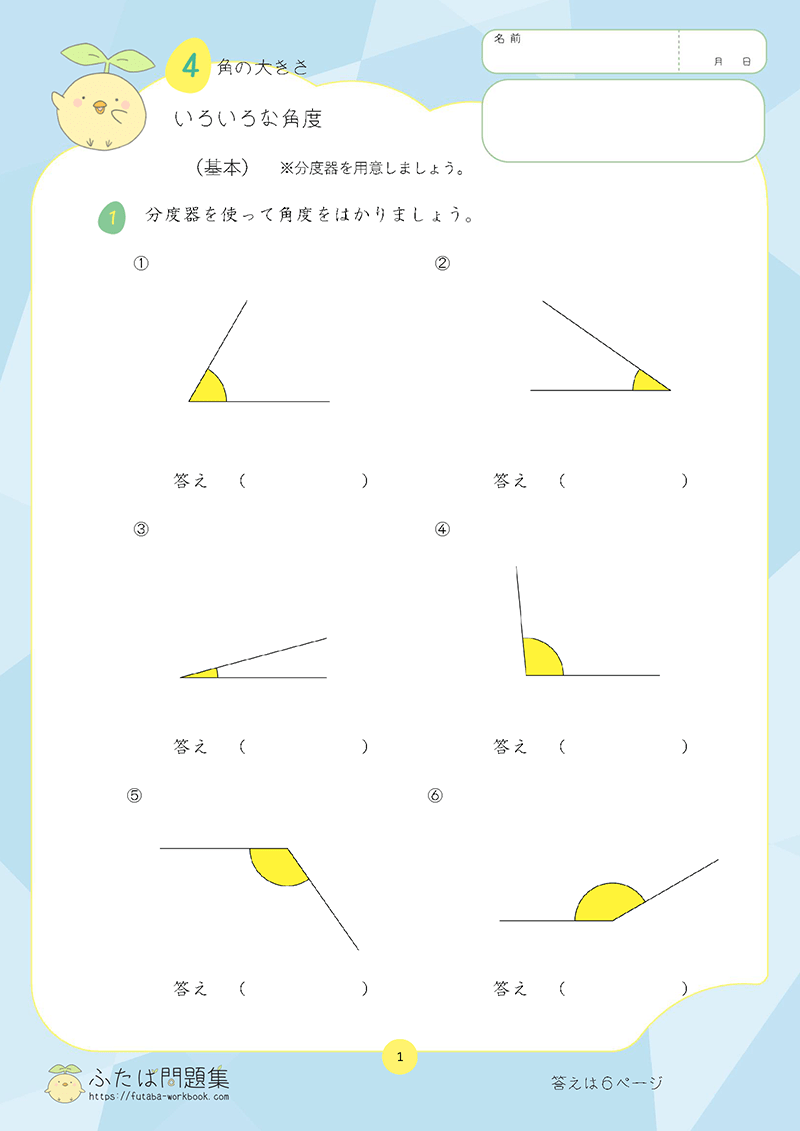
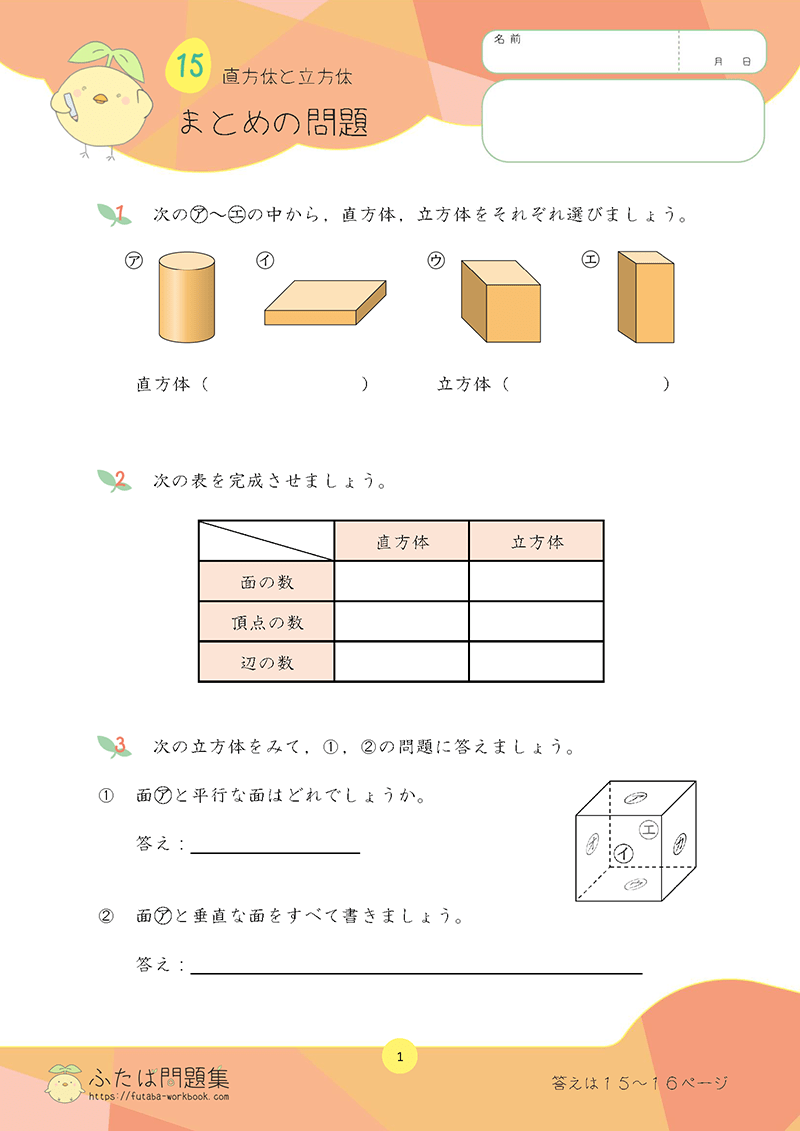
7日目:四角形と三角形の面積
5年生では、三角形、平行四辺形、ひし形、台形の面積の求め方について学習しました。
春休み中に「公式」を復習しましょう。
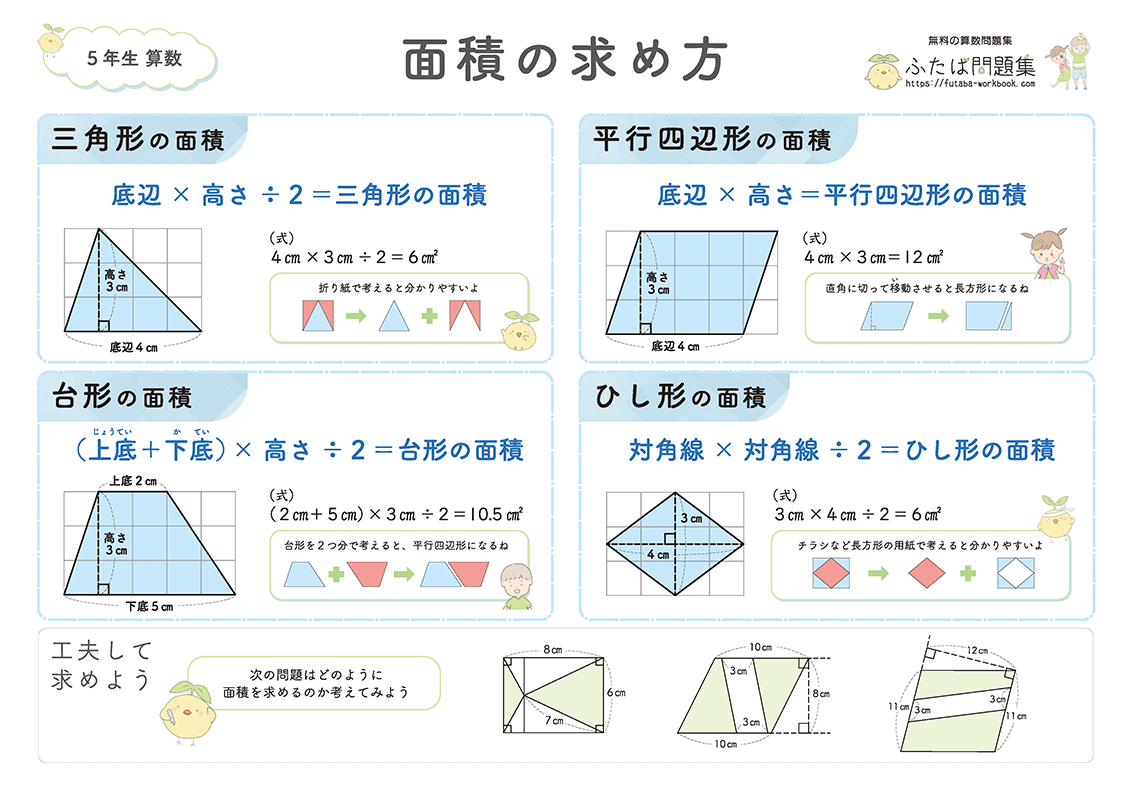
図形が苦手な場合は、折り紙や画用紙などを使って、図形を実際に作ってみましょう。
①理解チェックリスト
- 三角形、平行四辺形、ひし形、台形の面積の公式を言えるか
②公式を使って、図形の面積を求めよう
公式を理解したら、実際に様々な図形の面積を求める練習をしましょう。
練習問題を通して、公式の使い方が身につきます。
また、三角形や平行四辺形の面積を求める公式には、底辺と高さが用いられます。
「底辺をどこにするかによって、高さが変わること」を理解することも重要です。
もっとくわしく解説してほしい方は、こちらも動画を活用してください。
「ふたば問題集」は、小学校5年生の算数を効果的に復習できる充実した教材です。
基礎から応用まで幅広く対応し、子どもたちが楽しく学べる工夫が満載です。
算数の苦手意識を克服し、6年生の新年度準備に、ぜひ「ふたば問題集」を活用してみてください。
「ふたば問題集」で新年度準備をスタート
新年度に向けた学力アップには、「ふたば問題集」がおすすめです。
単元ごとに分かりやすく解説され、算数が苦手なお子さまも取り組みやすい内容です。
シンプルで見やすいページ構成が、集中力をサポートします。
無料で、必要な部分を印刷できるので、無駄なく活用できます。
新年度準備の第一歩として、今すぐダウンロードしてみませんか?
学年別 春休み進級準備のおすすめ
![]()
![]() 未就学児向け:【年長専用】親子で楽しむ!5日間でできる算数の入学準備
未就学児向け:【年長専用】親子で楽しむ!5日間でできる算数の入学準備
![]()
![]() 小学1年生:【小学1年生】ゲーム感覚で楽しく!7日間で完成する春休み算数復習
小学1年生:【小学1年生】ゲーム感覚で楽しく!7日間で完成する春休み算数復習
![]()
![]() 小学2年生:【小学2年】算数のまとめが無料で完結!春休み7日間集中トレーニング
小学2年生:【小学2年】算数のまとめが無料で完結!春休み7日間集中トレーニング
![]()
![]() 小学3年生:【3年生】1週間で完成!7日間算数復習プラン
小学3年生:【3年生】1週間で完成!7日間算数復習プラン
![]()
![]() 小学4年生:【4年生】習い事のスキマ時間活用!7日間算数復習スケジュール
小学4年生:【4年生】習い事のスキマ時間活用!7日間算数復習スケジュール
![]()
![]() 小学5年生:【5年生】7日間で完了!無料版算数復習法
小学5年生:【5年生】7日間で完了!無料版算数復習法