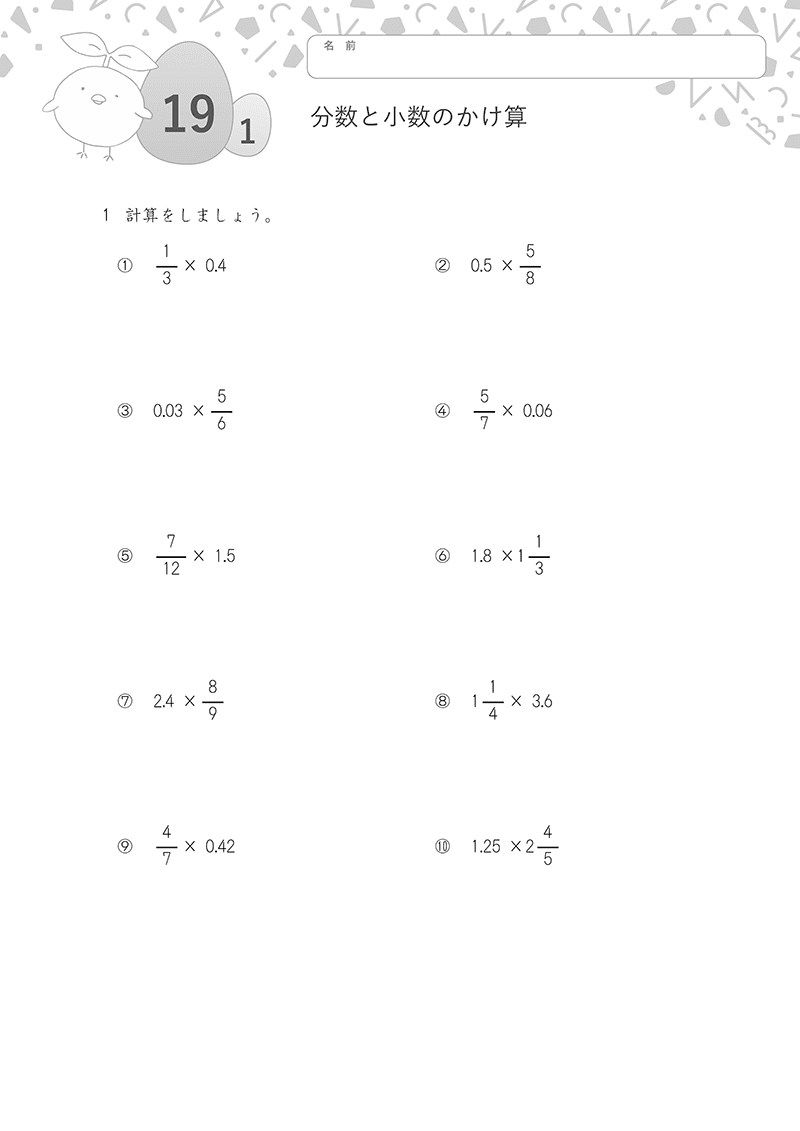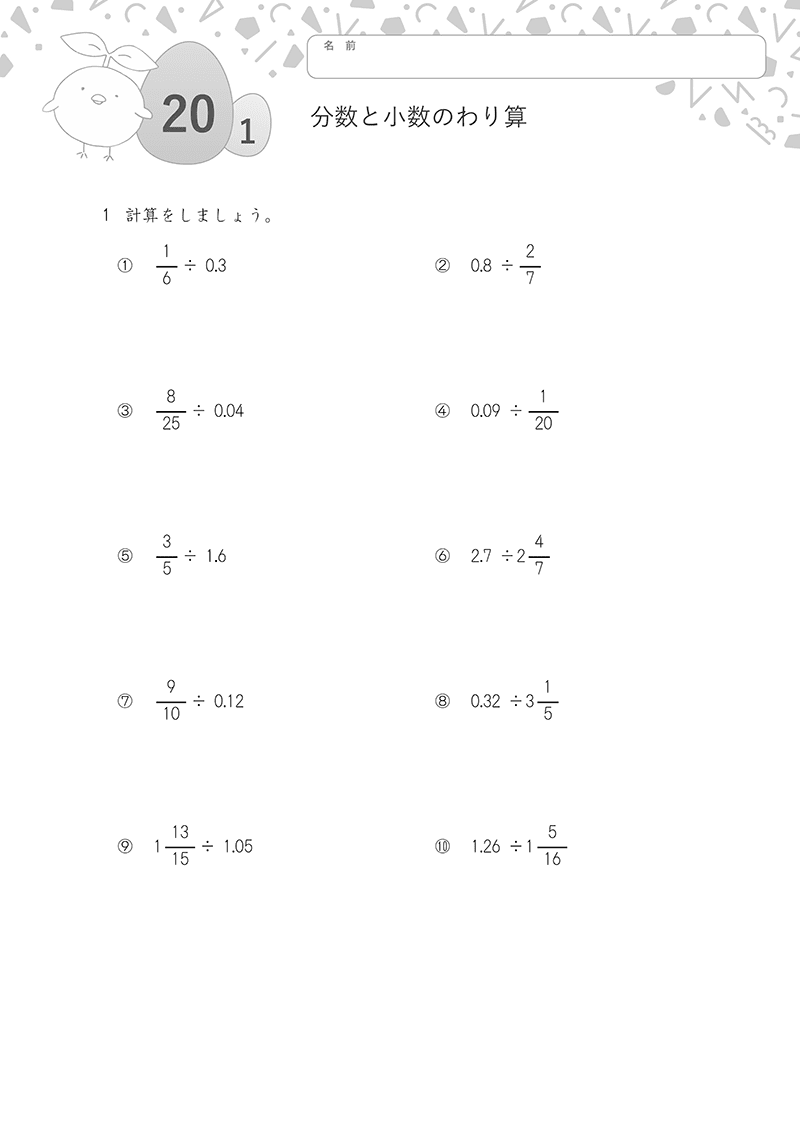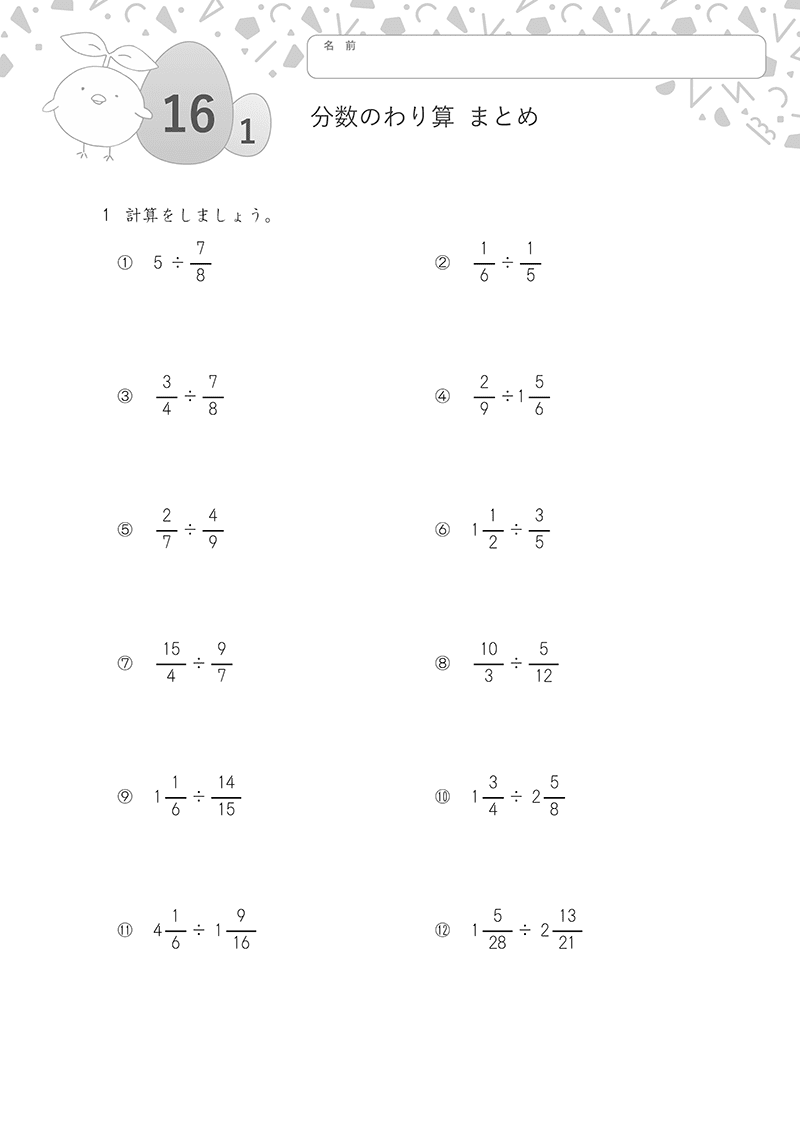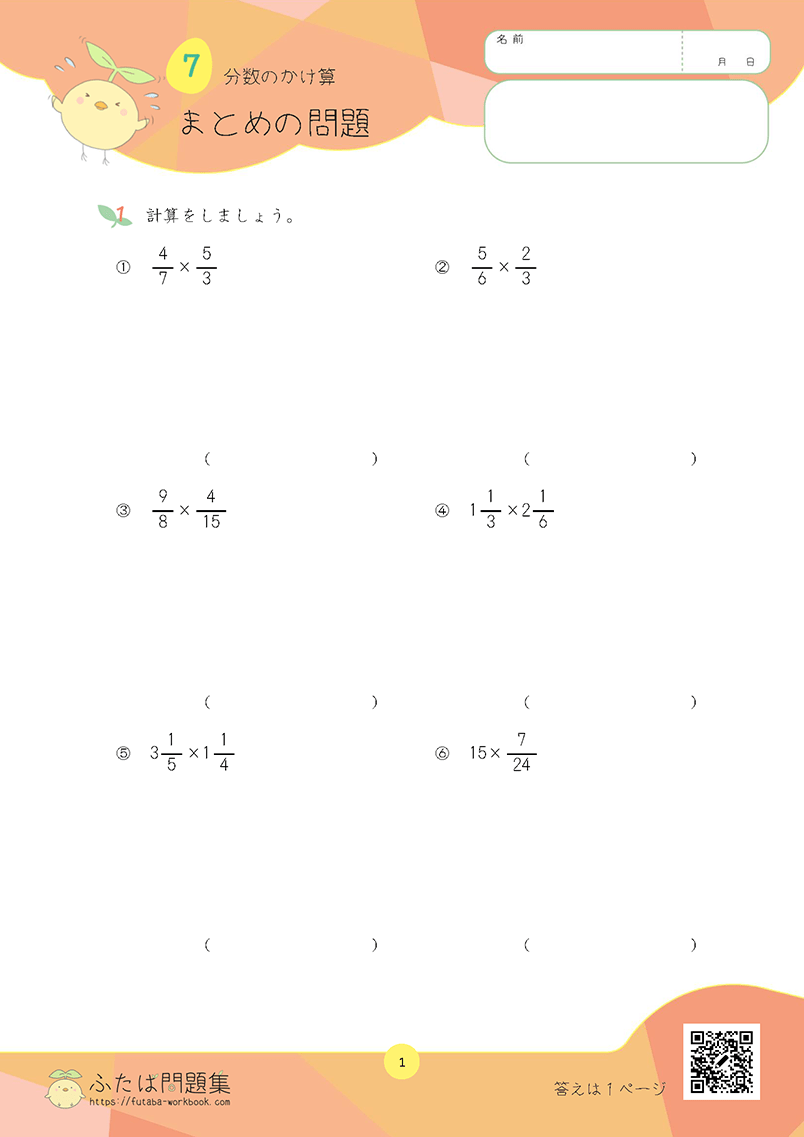「中学校に入学するのが楽しみな一方で、算数に苦手意識があるお子さんも少なくありません。
春休みに効率よく算数を復習するなら、中学1年生の数学を意識することが大切です。
今回は、6年生が中学生準備をするために最適な算数総復習プログラムを紹介します。
短期間で確実にレベルアップするポイントを押さえて、復習と予習を同時に完了させましょう。
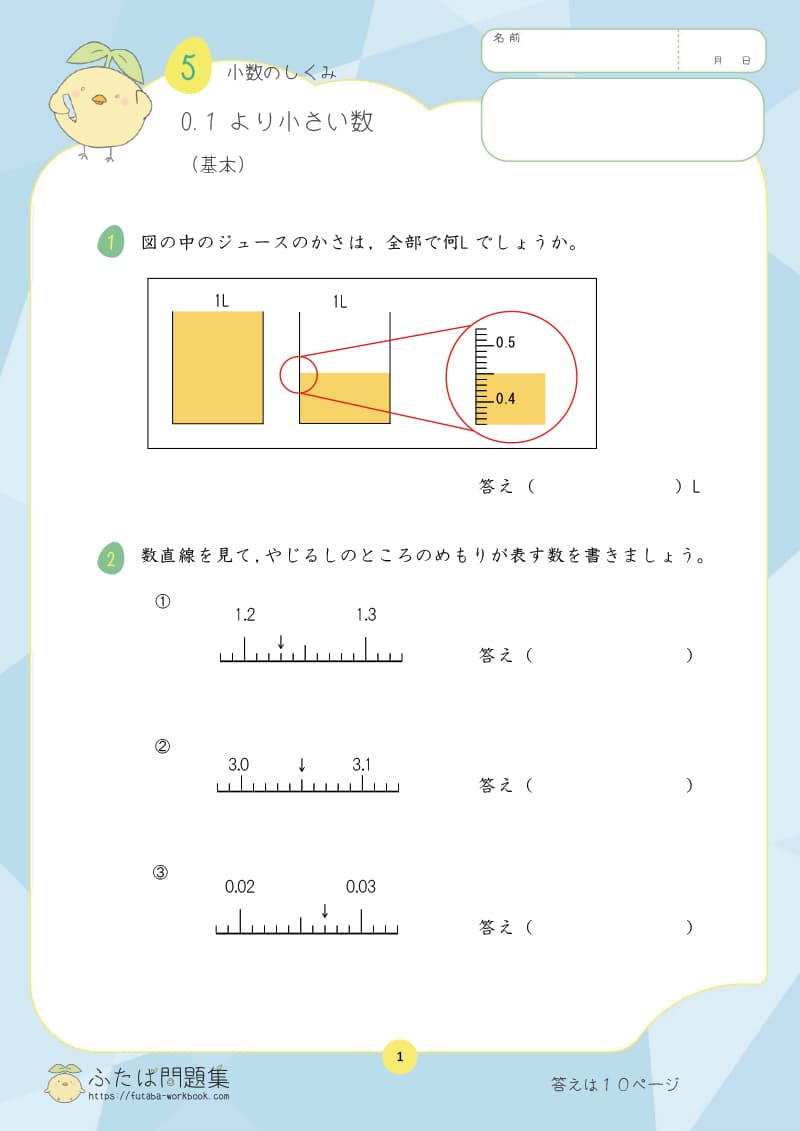
1日目：数直線と数の大小（5年生）
中学1年生の数学では、最初に「正負の数」を学習します。
「正負の数」とは、「プラス・マイナス」のことで、中学校からは、0より小さい数も扱うようになります。
小学校で学習した「数直線」や「数の大小」が土台になるため、しっかり復習しましょう。
①数直線
数直線は、数の大小を表すのに便利なツールです。
中学校の数学でも活用するので、使い慣れておきましょう。
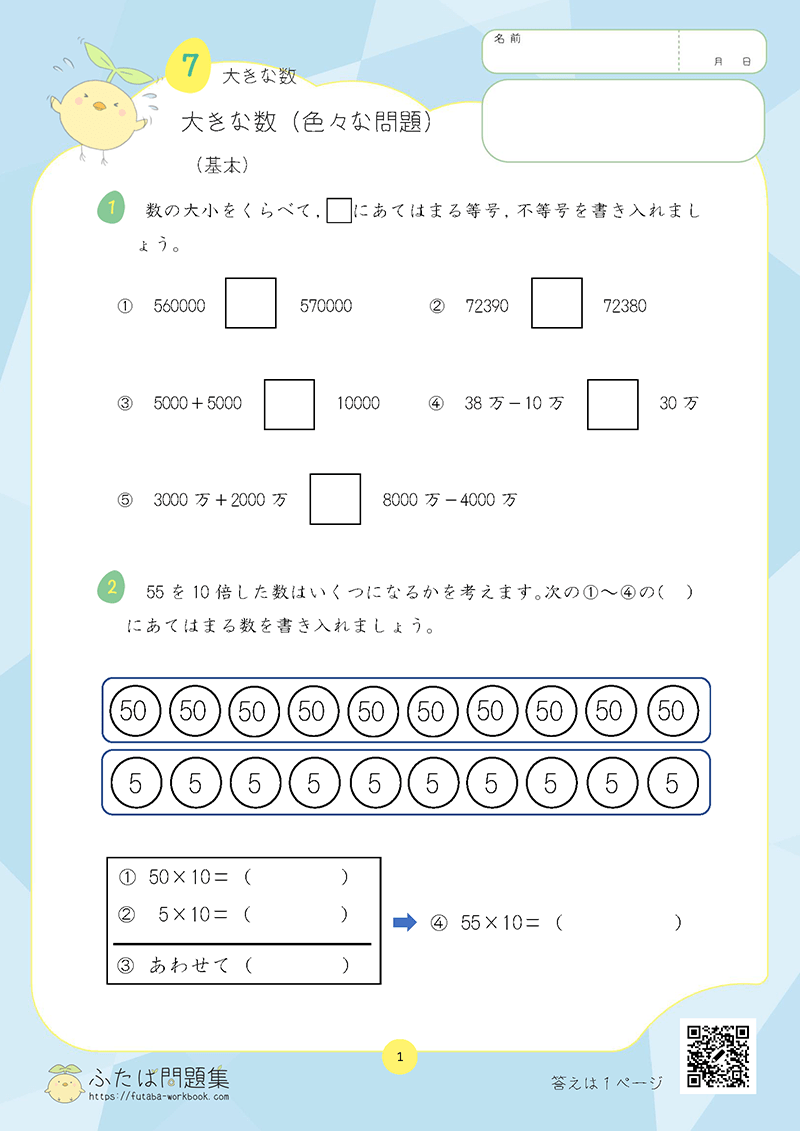
②数の大小比較
春休み中に、0より大きい数の大小関係をしっかり理解しておくことが大切です。
不等号や並び替えなどで、正しく大小比較をできるようにしましょう。
③予習のポイント
生活の中にある「負の数（0より小さい数）」を意識して探しながら、「正負の数」を予習しておきましょう。
【例】
- 冷凍食品を買う時に「冷凍食品は-18℃以下で保存する必要があります」などの注意書きを読んでもらう
- 気温がマイナスの場合、「天気予報で北海道の気温は何度って言っていた？」と質問する
- ゴルフに興味がありそうな場合、テレビを見ながら「スコアが-3のプレーヤーはパーより3打少ないという意味だよ」などと会話する
２日目：倍数・約数（5年生）
中学1年生では「素数」や「素因数分解」を学習します。
「素数」は、1とその数自身以外に正の約数を持たない、1より大きい自然数のことです。
- 2、3、5、7、11、13などは素数
- 1は素数ではない
- 4や6などは、1とその数自身以外に正の約数を持つため、素数ではない
「素因数分解」は、自然数を素数の積の形に表すことです。
例えば、12は 2 × 2 × 3 となり、これが12の素因数分解です。
これらの学習は5年生の「倍数・最小公倍数」「約数・最大公約数」とつながっているため、復習しておきましょう。
①倍数・最小公倍数
「倍数・最小公倍数」を復習することは、素因数分解の予習にもなります。
例えば、素因数分解「30 =2×3×5」を見ると、「30は2、3、5の倍数」とわかります。
そのため、しっかり理解しておくことが大切です。
②約数・最大公約数
素数は約数が2つしかない数です。
そのため、約数を理解しておけば、素数もスムーズに理解できるでしょう。
③予習ポイント
「素数」の意味が理解できたら「素数カルタ」で遊んでみましょう。
素数が書かれたカードを使って、カルタのルールで遊ぶゲームです。
素数を素早く見つける能力が試されます。
３日目：小数の計算（5・6年生）
中学1年生の数学では、「正負の数」を理解したあとに「正負の数の計算」を学習します。
まずは小数の計算を復習しましょう。
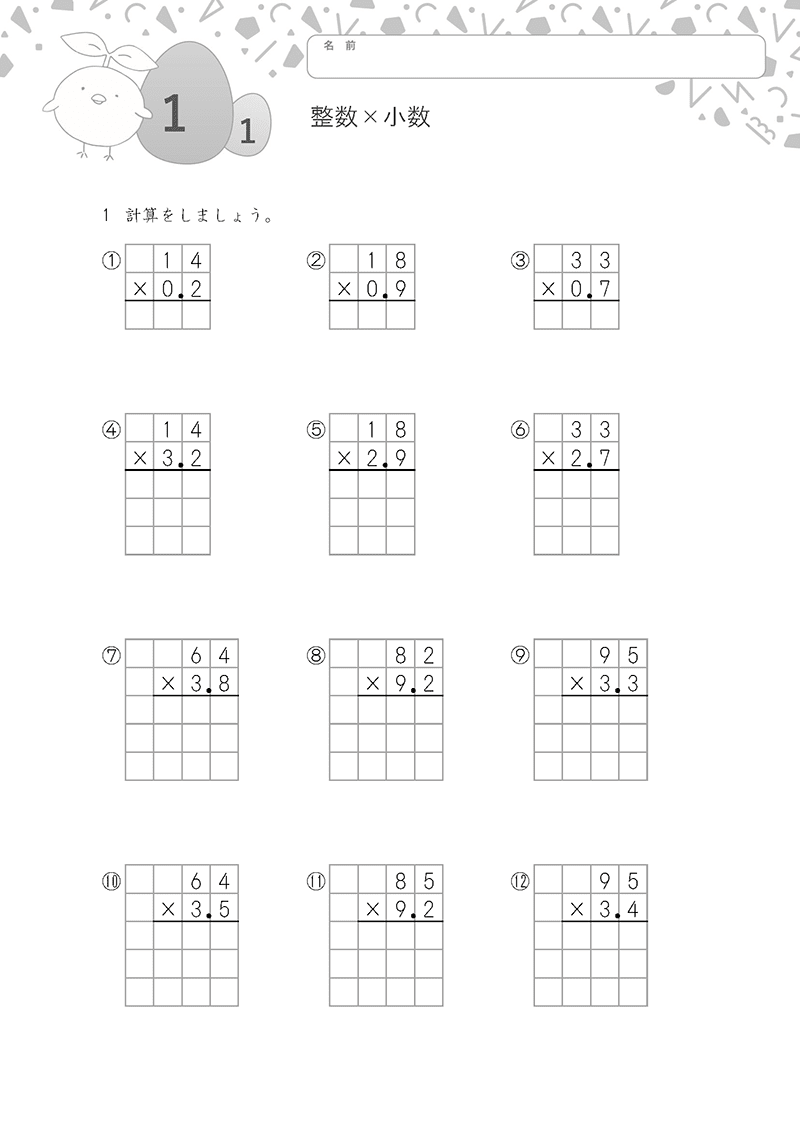
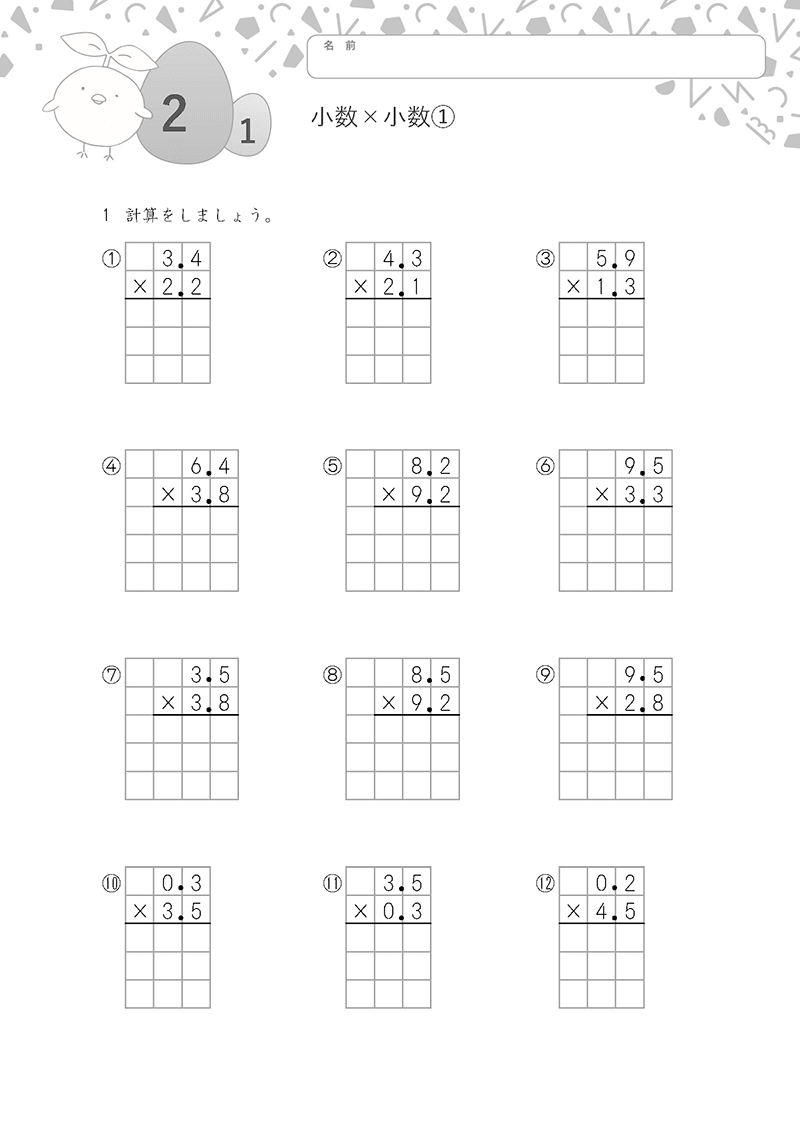
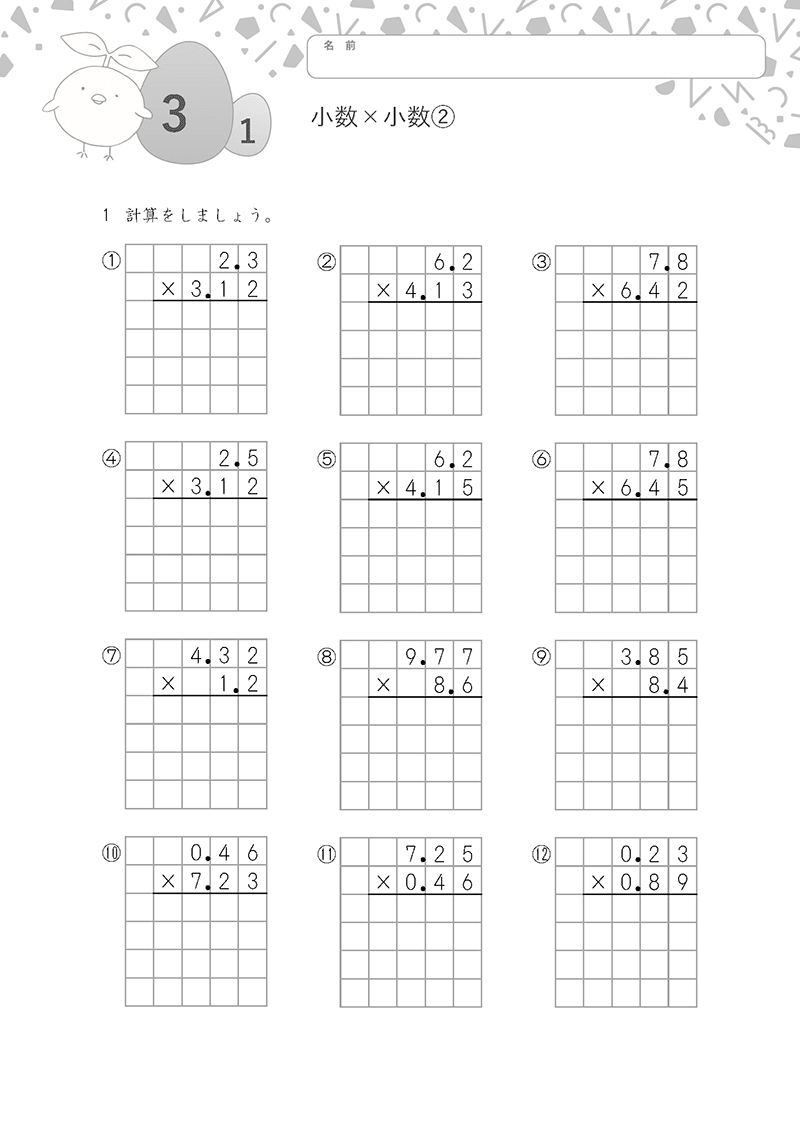
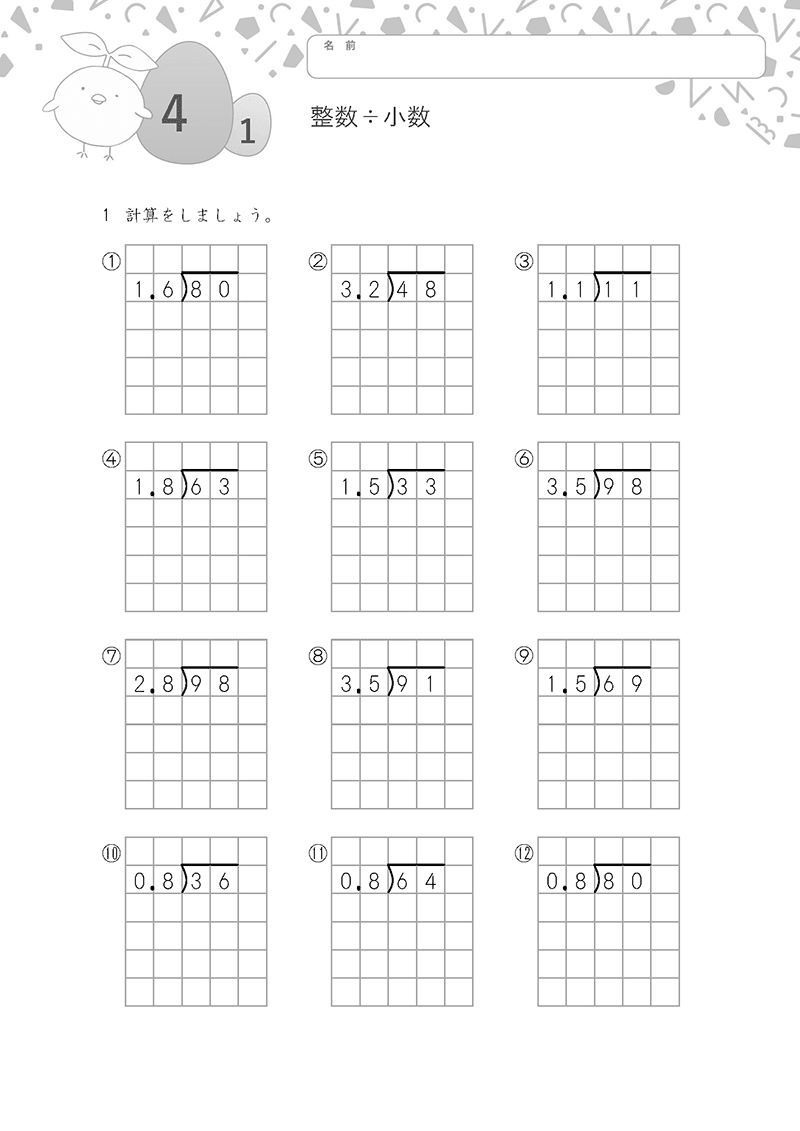
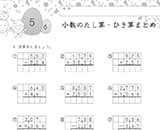
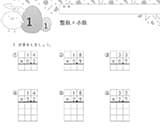
①小数・整数の計算
小数点に注意しながら、計算しましょう。
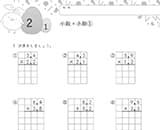
②小数・分数の計算
計算力アップは、くり返し練習することが上達の鍵です。
タイマーをセットして時間を測ったり、目標正解数を決めたりしながら、楽しく取り組みましょう。
4日目：分数の計算と逆数（6年生）
3日目と同じように、小数・分数・整数の計算は中学校の数学の土台になります。
春休み中に、分数の計算をマスターしておきましょう。
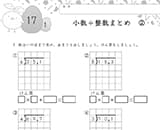
①分数の計算
「約分」に気をつけながら、分数の計算をしましょう。
②逆数
「逆数」とは、ある数にかけると1になる数のことです。
- 例えば、2の逆数は1/2です。なぜなら、2 × 1/2 = 1 となるからです。
- 分数の場合、分子と分母を入れ替えると逆数になります。
- 整数の逆数は、その整数を分母とした分数になります。 例えば、3の逆数は1/3です。
③予習ポイント
簡単でいいので「負の数の計算」に慣れておくことは大切です。
例えば「英語を言ってはいけないゲーム」。
「生活の中で英語のワードを言ったらマイナス2点、ことわざや四字熟語を使えたらプラス1点」というルールを設定すれば、遊びながら「負の数の計算」ができます。
移動時間などに遊んでみてください。
5日目：計算の工夫（4年生）
「正負の数」の学習では、いろんな計算の問題が登場します。
- かけ算の交換法則
- かけ算の結合法則
- 3 つ以上の数のかけ算
- 分配法則
これらの学習には、算数で学習した「計算の工夫」が役立ちます。
春休み中にしっかり復習しておきましょう。
①交換法則
「交換法則」とは、「かけ算の順番を入れ替えても、計算結果が変わらない」という法則です。
例えば、
- 2 × 3 = 6
- 3 × 2 = 6
のように、かけ算の順番を入れ替えても、結果はどちらも「6」になります。
では、「12×11×5 」を交換法則を使って解いてみましょう。
- 12×11×5
- 12×5 ×11
- （12×5） ×11
- 60×11＝660
このように、計算を楽にしたりするために役立ちます。
②結合法則
「結合法則」とは、「かけ算をする順番を変えても、計算結果が変わらない」という法則です。
例えば、
- (2 × 3) × 4 = 6 × 4 = 24
- 2 × (3 × 4) = 2 × 12 = 24
のように、かけ算をする順番を変えても、結果はどちらも「24」になります。
③分配法則
「分配法則」とは、かけ算と足し算（または引き算）が組み合わさった式を計算する際に役立つ法則です。
具体的には「a × (b + c) = (a × b) + (a × c) 」のように、式を展開します。
例えば「9×99」で考えてみましょう。
「分配法則」を使えば、筆算なしで答えを導き出せるのです。
- 9×99
- 9×（100-1）
- (9× 100) – (9 × 1)
- 900-9
中学校で学習する「分配法則」は、数字だけでなく、文字式にも活用されます。
しっかり復習しておきましょう。
6日目：変わり方調べ・割合・速さ（5年生）
「正負の数」の次の単元は、「文字を使った式」方程式と続きます。
「x」「y」を使って問題を解くため、むずかしいと感じるかもしれません。
けれども、算数の学習をしっかり復習していれば、問題ないのでご安心ください。
①変わり方調べ
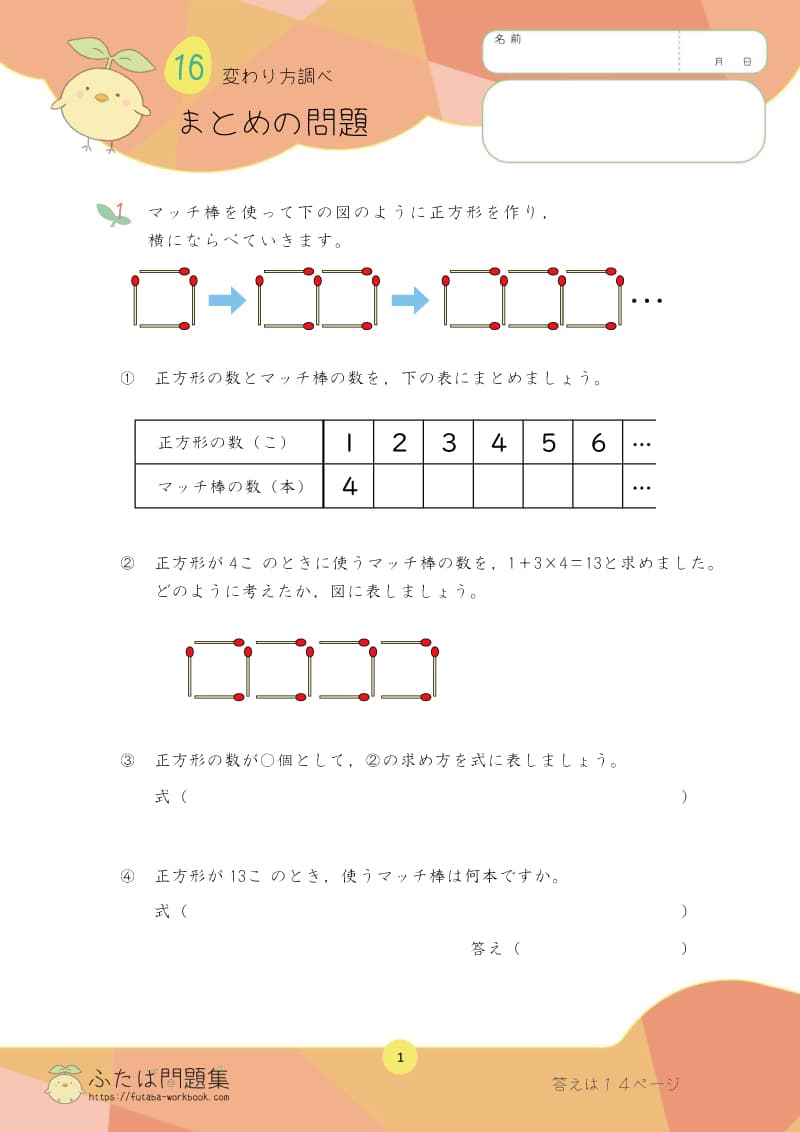
「マッチ棒を使って正方形をつなげたときの棒の本数を求める活動」は5年生の「変わり方調べ」で学習しました。
この問題を文字を使った式で考える学習を中学1年生で学習します。
春休み中に基礎問題をしっかりマスターしておきましょう。
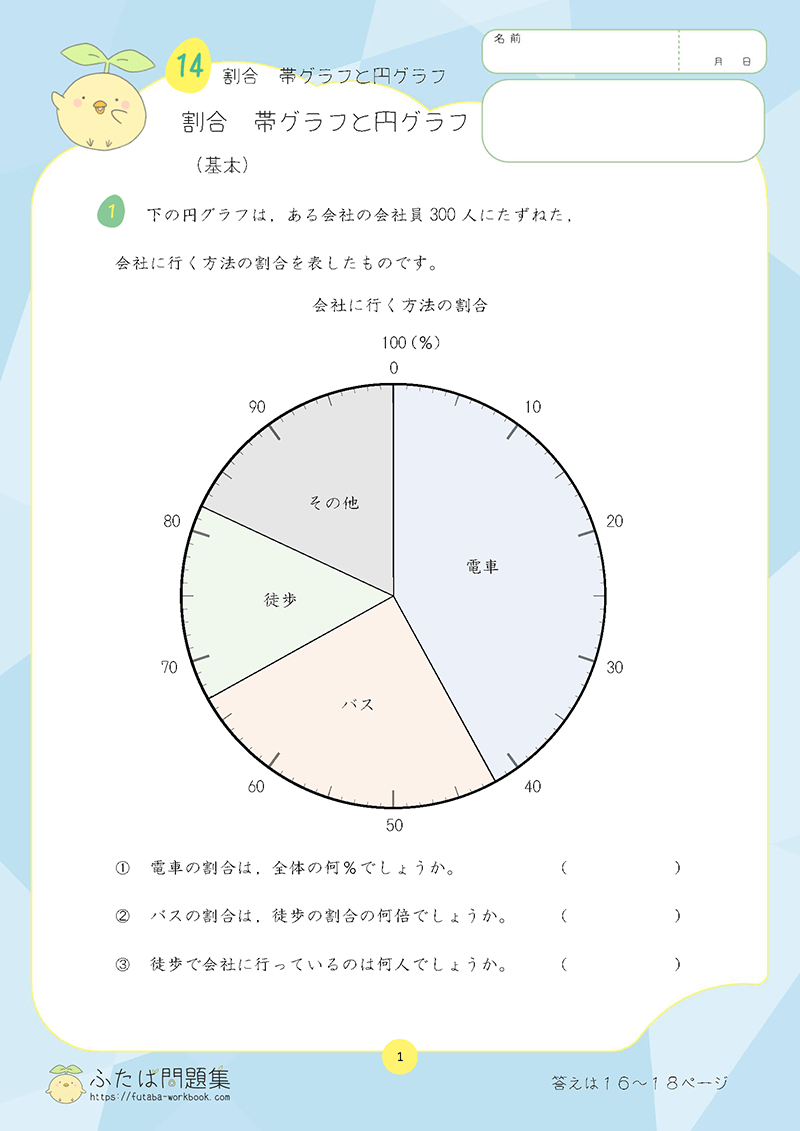
②割合
中学1年生の数学では、文字を使って「割合」を求める学習をします。
百分率を復習しておくことをおすすめします。
③速さ
文字を使って「速さ」を求める学習もするため、しっかり復習しておきましょう。
7日目：文字と式
6年生で学習した「文字と式」を最後に復習しましょう。
①文章問題を読み解く練習
文章問題のポイントは次の通りです。
- 「この問題では何を求めるのか」を明確にする、もしくは線を引いておく
- 問題文にある「数字」と「文字」に注目する
「文字」があっても、これまで学習した計算方法と同じです。
焦らず、自信をもって、取り組みましょう。
②文字を使った計算の工夫
「かっこ」を使った計算のルールを理解していると、文字式の扱いがスムーズになります。
「交換法則」「結合法則」「分配法則」をもう一度復習しましょう。
中学校の入学準備期間は、思ったより短いものです。
「数学の予習を意識した復習をしたい」「効率よく楽しく勉強したい」なら、ふたば問題集がおすすめです。
今回紹介した復習プランを活用しながら入学準備をして、晴れやかな笑顔で中学校の門をくぐりましょう。
「ふたば問題集」で新年度準備をスタート
新年度に向けた学力アップには、「ふたば問題集」がおすすめです。
単元ごとに分かりやすく解説され、算数が苦手なお子さまも取り組みやすい内容です。
シンプルで見やすいページ構成が、集中力をサポートします。
無料で、必要な部分を印刷できるので、無駄なく活用できます。
新年度準備の第一歩として、今すぐダウンロードしてみませんか？
未就学児向け：
